ชั้นเรียนกระบวนการ
การแสดงออกทางกราฟิก
การคิด
การแสดงออกที่มีโครงสร้าง
หมายเหตุ
การแสดงออกอย่างมีประสิทธิภาพ
ทรีแมป
แผนภาพวงเล็บ
โหมดเริ่มต้น
ในศตวรรษที่ 19 นักคณิตศาสตร์ชาวอังกฤษ จอห์น เวนน์ ได้ประดิษฐ์เครื่องมือสำหรับแสดงความสัมพันธ์ของเซตโดยใช้กราฟิกทางเรขาคณิต ซึ่งก็คือ แผนภาพเวนน์ กราฟประเภทนี้ซึ่งใช้วงกลมทับซ้อนกันเพื่อแสดงจุดตัด การรวม และส่วนประกอบของเซต ไม่เพียงแต่กลายมาเป็นเครื่องมือพื้นฐานในสาขาคณิตศาสตร์เท่านั้น แต่ยังแสดงให้เห็นถึงความสามารถในการใช้งานที่มีประสิทธิภาพในการใช้เหตุผลเชิงตรรกะ สถิติความน่าจะเป็น และการวิเคราะห์ข้อมูลอีกด้วย บทความนี้จะวิเคราะห์คุณค่าหลักของแผนภาพเวนน์ในทางคณิตศาสตร์อย่างเป็นระบบจาก 5 มิติ ได้แก่ คำจำกัดความ สถานการณ์การประยุกต์ใช้ทางคณิตศาสตร์ กรณีทั่วไป เครื่องมือการผลิต และวิธีการวาด
แผนภาพเวนน์แสดงความสัมพันธ์เชิงตรรกะระหว่างชุดต่างๆ ในรูปแบบภาพผ่านทางพื้นที่วงกลมหรือวงรีที่ทับซ้อนกัน องค์ประกอบหลักประกอบด้วย:
การแทนค่าชุด: วงกลมแต่ละวงแทนชุดอิสระ และพื้นที่ภายในวงกลมคือองค์ประกอบของชุด
จุดตัด (∩) : พื้นที่ทับซ้อนแสดงถึงองค์ประกอบทั่วไปของชุดสองชุดหรือมากกว่า
สหภาพ (∪) : พื้นที่ทั้งหมดที่ครอบคลุมโดยวงกลมทั้งหมดแสดงถึงผลลัพธ์ของสหภาพของชุด
ส่วนเติมเต็ม: พื้นที่ภายในกล่องสี่เหลี่ยม (โดเมน) ที่ไม่ครอบคลุมโดยวงกลม หมายถึงองค์ประกอบที่ไม่เป็นส่วนหนึ่งของเซตใดๆ
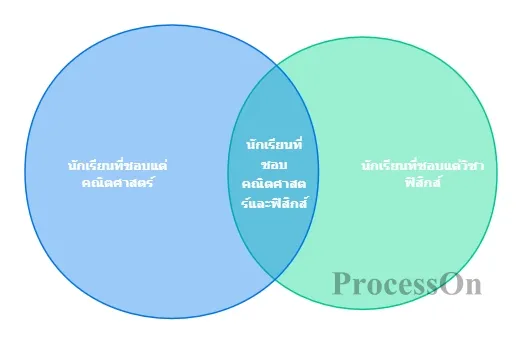
ตัวอย่างเช่น ในแผนภาพเวนน์ของเซต A (นักเรียนที่ชอบคณิตศาสตร์) และเซต B (นักเรียนที่ชอบฟิสิกส์) ส่วนที่ทับซ้อนกันแสดงถึง "นักเรียนที่ชอบทั้งคณิตศาสตร์และฟิสิกส์" และส่วนที่ไม่ทับซ้อนกันแสดงถึง "นักเรียนที่ชอบเฉพาะคณิตศาสตร์" และ "นักเรียนที่ชอบเฉพาะฟิสิกส์" ตามลำดับ
1. การดำเนินการชุดที่ใช้งานง่าย
ไดอะแกรมเวนน์แปลงการดำเนินการชุดนามธรรมเป็นการดำเนินการทางภาพ ตัวอย่างเช่น เมื่อพิสูจน์กฎของเดอมอร์แกน ((A∪B)' = A'∩B') ความเท่ากันสามารถตรวจยืนยันได้ด้วยภาพโดยการพล็อตส่วนเติมเต็มและส่วนตัดกันของสองเซต วิธีการพิสูจน์เชิงกราฟิกนี้ใช้กันอย่างแพร่หลายในการศึกษาคณิตศาสตร์ระดับประถมศึกษา เพื่อช่วยให้นักเรียนก้าวข้ามอุปสรรคทางความคิดของตรรกะเชิงสัญลักษณ์
2. เครื่องมือสร้างแบบจำลองสำหรับปัญหาความน่าจะเป็น
ในทฤษฎีความน่าจะเป็น ไดอะแกรมเวนน์เป็นเครื่องมือที่มีประสิทธิภาพในการแก้ปัญหาเหตุการณ์อิสระ เหตุการณ์ที่แยกกัน และความน่าจะเป็นแบบมีเงื่อนไข ตัวอย่างเช่น เมื่อคำนวณความน่าจะเป็นของ "การทอยลูกเต๋าแล้วได้เลขคู่ที่มากกว่า 3" เราสามารถหาค่าความน่าจะเป็นของพื้นที่จุดตัด {4,6} ได้โดยตรงโดยการวาดแผนภาพเวนน์ของเหตุการณ์ A (เลขคู่: {2,4,6}) และเหตุการณ์ B (>3: {4,5,6}) งานวิจัยจากมหาวิทยาลัยเคมบริดจ์แสดงให้เห็นว่านักเรียนที่ใช้แผนภาพเวนน์มีประสิทธิภาพในการแก้ปัญหาความน่าจะเป็นเพิ่มขึ้น 40%
3. กรอบแนวคิดในการอนุมานของข้อเสนอเชิงตรรกะ
ไดอะแกรมเวนน์สามารถเปลี่ยนแปลงข้อเสนอเชิงตรรกะ เช่น "A ทั้งหมดคือ B" และ "ไม่มี A ที่เป็น C" ให้เป็นความสัมพันธ์ทางเรขาคณิตได้ ตัวอย่างเช่นในการใช้เหตุผลแบบซิลโลจิสติกว่า "โลหะทั้งหมดเป็นตัวนำ ทองแดงเป็นโลหะ ดังนั้น ทองแดงจึงเป็นตัวนำ" การวาดวงกลมความสัมพันธ์การรวมระหว่าง "โลหะ" และ "ตัวนำ" จะทำให้สามารถตรวจยืนยันความจำเป็นของข้อสรุปได้อย่างรวดเร็ว วิธีการให้เหตุผลเชิงกราฟิกนี้ยังใช้กันอย่างแพร่หลายในสาขาต่างๆ เช่น พีชคณิตแบบบูลีนและการเพิ่มประสิทธิภาพการค้นหาฐานข้อมูลในวิทยาการคอมพิวเตอร์
สถิติการเลือกหลักสูตรของนักศึกษา
จากนักเรียน 50 คนในชั้นเรียน มี 28 คนเลือก แข่งขัน คณิตศาสตร์ 23 คนเลือกแข่งขัน เคมี และ 5 คนไม่ได้เข้าร่วมการแข่งขันใดๆ เลย สามารถสร้างแบบจำลองต่อไปนี้ได้โดยใช้แผนภาพเวนน์:
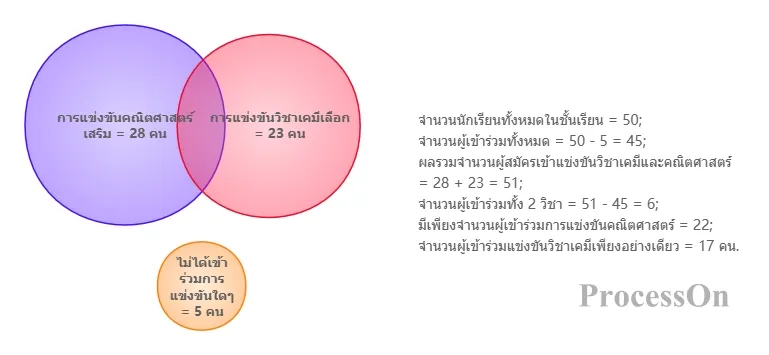
สถิติการเลือกหลักสูตรของนักศึกษา - แผนภาพเวนน์
จำนวนผู้เข้าร่วมทั้งหมด = 50 - 5 = 45;
วิชาเคมี และคณิตศาสตร์ = 28 + 23 = 51;
จำนวนผู้เข้าร่วมทั้ง 2 วิชา = 51 - 45 = 6.
แผนภาพเวนน์สุดท้ายแสดงให้เห็นว่า มีผู้เข้าร่วมการแข่งขัน คณิตศาสตร์ เท่านั้น 22 คน เข้าร่วมการแข่งขันเท่านั้น 17 คน และ 6 คนเข้าร่วมในทั้งสองวิชา กรณีนี้พิสูจน์ประสิทธิภาพของแผนภาพเวนน์ในการแก้ปัญหา "การนับทับซ้อน"
PPT/SmartArt: เหมาะสำหรับการวาดไดอะแกรมเวนน์อย่างรวดเร็วของชุดข้อมูล 2-3 ชุด คุณสามารถสร้างกราฟิกขั้นพื้นฐานได้ผ่านทาง "แทรก → SmartArt → ความสัมพันธ์ → ไดอะแกรมเวนน์พื้นฐาน" ซึ่งรองรับการปรับสีและความโปร่งใส
ภาษา Origin/R: เมื่อต้องจัดการกับชุดข้อมูลที่ซับซ้อนมากกว่าสามชุด ปลั๊กอิน Venn Diagram ของ Origin หรือแพ็กเกจ ggVennDiagram ของภาษา R สามารถสร้างกราฟิกที่มีความแม่นยำสูงได้
เครื่องมือออนไลน์: ProcessOn ที่ไม่จำเป็นต้องกรอกข้อมูลและ รองรับ การลาก กราฟิก ไปยัง ผืน ผ้าใบ โดยตรง เหมาะสำหรับผู้ใช้ที่ไม่มีความรู้ด้านการเขียนโปรแกรม
ต่อไป เราจะแนะนำวิธีการวาดแผนภาพเวนน์ โดยใช้ ProcessOn เป็นตัวอย่าง :
กำหนดชุด: เข้าสู่เพจไฟล์ ProcessOn สร้างแผนผังกระแสข้อมูลใหม่ และ ระบุชุดที่จะวิเคราะห์ (เช่น หัวเรื่อง A, หัวเรื่อง B);
วาดรูปทรงพื้นฐาน: คลิก "รูปทรงเพิ่มเติม" ทางด้านซ้าย เลือกไดอะแกรมเวนน์ ลาก วงกลม สอง วงจากพื้นที่รูปทรงไปที่ผืนผ้าใบ และปรับตำแหน่งเพื่อให้ซ้อนทับกันบางส่วน
พื้นที่การทำเครื่องหมาย: เติมพื้นที่ที่ไม่ทับซ้อนกันและพื้นที่จุดตัดด้วยสีต่างๆ และเพิ่มป้ายปริมาณองค์ประกอบ
เพิ่มประสิทธิภาพการแสดงผล: ปรับ สี ความโปร่งใส ฯลฯ และเพิ่มคำอธิบายข้อความ เช่น "เฉพาะ A" "เฉพาะ B" "A∩B" เป็นต้น
ดาวน์โหลดหรือแชร์: หลังจากวาดแผนภาพเวนน์แล้ว คุณสามารถคลิกปุ่มดาวน์โหลดที่มุมขวาบนเพื่อส่งออกเป็นรูปภาพ PDF หรือรูปแบบอื่น หรือสร้างลิงก์ออนไลน์เพื่อแชร์กับผู้อื่นได้
แม้ว่าแผนภาพเวนน์จะมีข้อได้เปรียบคือใช้งานง่าย แต่ควรทราบข้อจำกัดด้วย:
ข้อจำกัดของจำนวนชุด: ไดอะแกรมเวนน์แบบดั้งเดิมสามารถแสดงชุดข้อมูลได้อย่างชัดเจนถึง 5 ชุด หากจำนวนเกินกว่านี้ ขอแนะนำให้ใช้ไดอะแกรม UpSet แทน
ความเสี่ยงของการบิดเบือนพื้นที่: พื้นที่ของวงกลมอาจไม่เป็นสัดส่วนกับขนาดของชุด และต้องระบุจำนวนองค์ประกอบเฉพาะไว้ในรูปภาพ
ไม่สามารถใช้ได้กับข้อมูลต่อเนื่อง: สำหรับข้อมูลต่อเนื่อง เช่น ลำดับเวลา การเปลี่ยนแปลงอุณหภูมิ ฯลฯ คุณจะต้องใช้แผนภูมิเส้นหรือแผนที่ความร้อนแทน
จากการดำเนินการชุดในห้องเรียนไปจนถึงการวิเคราะห์เชิงอนุพันธ์ในจีโนมิกส์ แผนภาพเวนน์ซึ่งมีภาษาทางเรขาคณิตที่กระชับ ช่วยแปลงตรรกะทางคณิตศาสตร์เชิงนามธรรมให้กลายเป็นแบบจำลองภาพที่รับรู้ได้ เนื่องจากความซับซ้อนของข้อมูลเพิ่มมากขึ้น การประยุกต์ใช้งานแบบบูรณาการของไดอะแกรมเวนน์ ไดอะแกรม UpSet ไดอะแกรมแผนผังต้นไม้ และเครื่องมืออื่นๆ กำลังผลักดันให้การแสดงภาพทางคณิตศาสตร์พัฒนาไปสู่มิติที่สูงขึ้น สำหรับผู้เรียน การฝึกฝนการวาดและการใช้ไดอะแกรมเวนน์ไม่เพียงแต่เป็นการฝึกฝนเครื่องมือเท่านั้น แต่ยังเป็นวิธีการสำคัญในการปลูกฝังการคิดอย่างมีโครงสร้างและความสามารถในการวิเคราะห์แบบสหวิทยาการอีกด้วย
แผนผังความคิดแบบร่วมมือกันออนไลน์ฟรี
