Руководство по диаграммам Венна : решение математических задач с помощью графики

В XIX веке британский математик Джон Венн изобрел инструмент для отображения взаимосвязей множеств с помощью геометрической графики — диаграмму Венна. Этот тип графика, использующий перекрывающиеся окружности для выражения пересечения, объединения и дополнения множеств, не только стал основным инструментом в области математики, но и продемонстрировал мощную практичность в логических рассуждениях, статистике вероятностей и анализе данных. В этой статье будет проведен систематический анализ основной ценности диаграммы Венна в математике с пяти точек зрения: определение, сценарии математического применения, типичные случаи, инструменты производства и методы рисования.

Ⅰ. Определение и основная логика диаграммы Венна

Диаграмма Венна наглядно представляет логическую взаимосвязь между несколькими множествами посредством перекрывающихся круговых или эллиптических областей. Его основные элементы включают в себя:

Представление множества: каждый круг представляет собой независимое множество, а область внутри круга является элементом множества;

Пересечение (∩): область перекрытия представляет собой общие элементы двух или более множеств;

Объединение (∪): Общая площадь, покрытая всеми кругами, представляет собой результат объединения множеств;

Дополнение: область внутри прямоугольной рамки (домен), не охваченная кругом, представляет собой элементы, которые не принадлежат ни одному множеству.

Например, на диаграмме Венна для набора A (ученики, которые любят математику) и набора B (ученики, которые любят физику) перекрывающаяся часть представляет «учеников, которые любят и математику, и физику», а неперекрывающаяся часть представляет «учеников, которые любят только математику» и «учеников, которые любят только физику» соответственно.

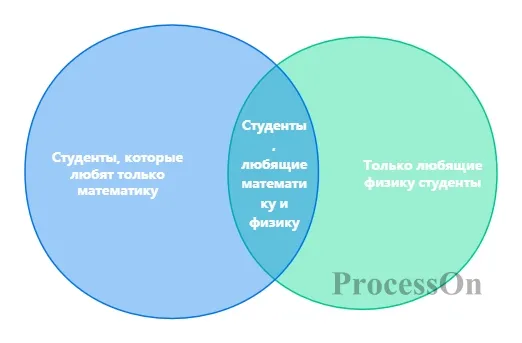
Ⅱ. Применение диаграммы Венна в математике

1. Интуитивные операции с множествами

Диаграммы Венна преобразуют абстрактные операции с множествами в визуальные операции. Например, при доказательстве закона Де Моргана ((A∪B)' = A'∩B') равенство можно визуально проверить, построив графики дополнения и пересечения двух множеств. Этот метод графического доказательства широко используется в начальном математическом образовании, чтобы помочь учащимся преодолеть когнитивные барьеры символической логики.

2. Инструменты моделирования вероятностных задач

В теории вероятностей диаграммы Венна являются мощным инструментом для решения задач на независимые события, взаимоисключающие события и условную вероятность. Например, при вычислении вероятности «броска игральной кости и выпадения четного числа, большего 3», мы можем напрямую получить значение вероятности области пересечения {4,6}, нарисовав диаграмму Венна события A (четное число: {2,4,6}) и события B (>3: {4,5,6}). Исследования Кембриджского университета показали, что студенты, использующие диаграммы Венна, на 40% эффективнее решали задачи на вероятность.

3. Структура вывода логических предложений

Диаграммы Венна могут преобразовывать логические предложения, такие как «все А есть В» и «ни одно А не есть С», в геометрические соотношения. Например, в силлогистическом рассуждении «все металлы являются проводниками, медь — металл, следовательно, медь — проводник», проведя круг отношения включения между «металлом» и «проводником», можно быстро проверить необходимость вывода. Этот метод графического рассуждения также широко используется в таких областях, как булева алгебра и оптимизация запросов к базам данных в информатике.

Ⅲ. Анализ типичных случаев в математике

Статистика выбора курсов студентами

Из 50 учеников класса 28 выбрали олимпиаду по математике , 23 — олимпиаду по химии , а 5 не участвовали ни в одной олимпиаде. С помощью диаграммы Венна можно построить следующую модель:

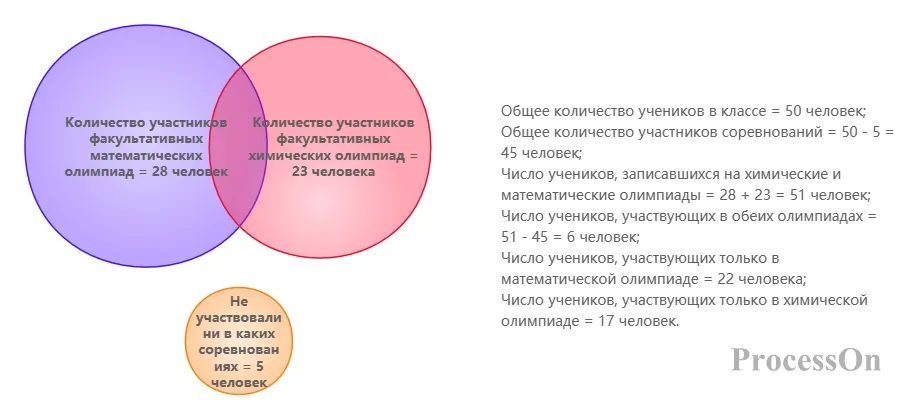
Статистика выбора курсов студентами - диаграмма Венна

Общее количество участников = 50 - 5 = 45;

химии и математике = 28 + 23 = 51;

Количество участников по обоим предметам = 51 - 45 = 6.

Итоговая диаграмма Венна показала: 22 человека участвовали только в математической олимпиаде, 17 человек участвовали только в олимпиаде и 6 человек участвовали в обоих предметах. Этот случай подтверждает эффективность диаграммы Венна при решении «задачи подсчета перекрытий».

IV. Инструмент для создания диаграммы Венна

PPT/SmartArt: подходит для быстрого рисования диаграмм Венна из 2-3 наборов данных. Вы можете создавать базовые графические объекты с помощью «Вставка → SmartArt → Связь → Базовая диаграмма Венна», которая поддерживает настройку цвета и прозрачности.

Язык Origin/R: При работе с более чем тремя наборами сложных данных подключаемый модуль диаграммы Венна Origin или пакет ggVennDiagram языка R могут генерировать высокоточную графику.

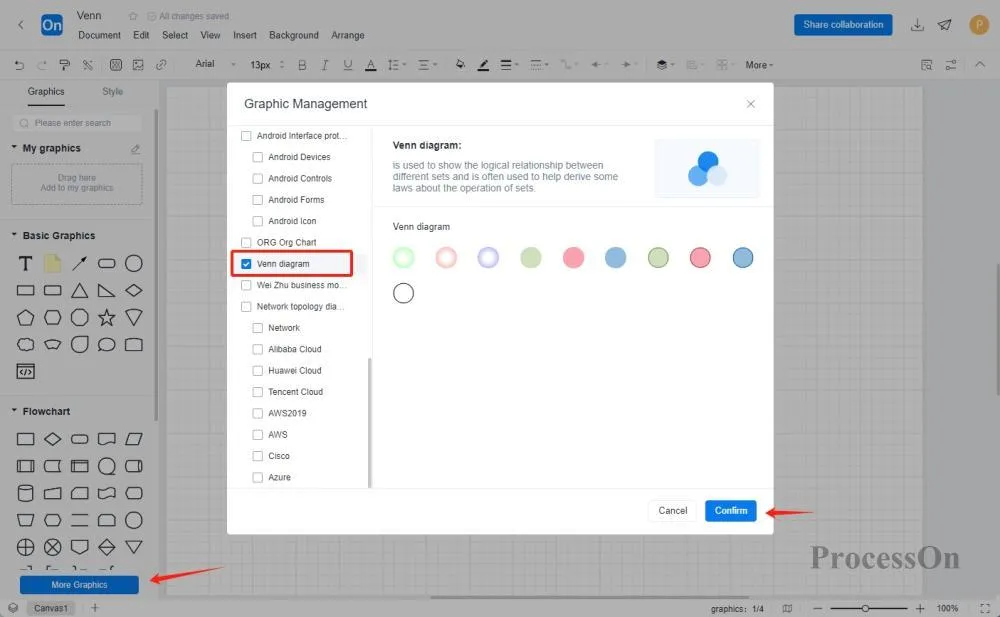
Онлайн-инструмент: ProcessOn, который не требует заполнения данных и поддерживает прямое перетаскивание графики на холст . Подходит для пользователей без навыков программирования.

Ⅴ. Как нарисовать диаграмму Венна

Далее , на примере ProcessOn , мы покажем, как нарисовать диаграмму Венна:

Определите набор: войдите на страницу файла ProcessOn, создайте новую блок-схему и укажите набор для анализа (например, субъект A, субъект B);

Создайте диаграмму Венна→

Нарисуйте базовые фигуры: нажмите «Другие фигуры» слева, выберите диаграмму Венна, перетащите два круга из области фигур на холст и отрегулируйте их положение так, чтобы они частично перекрывали друг друга;

Маркировка области: закрасьте непересекающиеся области и области пересечения разными цветами, добавьте метки количества элементов;

Оптимизируйте отображение: настройте цвет, прозрачность и т. д. , а также добавьте текстовые описания, такие как «только A», «только B», «A∩B» и т. д.

Загрузите или поделитесь: после того, как вы нарисуете диаграмму Венна, вы можете нажать кнопку загрузки в правом верхнем углу, чтобы экспортировать ее в изображение, PDF или другие форматы, или создать онлайн-ссылку для обмена с другими.

VI. Ограничения диаграмм Венна

Хотя диаграмма Венна имеет преимущество в том, что она интуитивно понятна, следует также отметить ее ограничения:

Ограничение на количество наборов: Традиционные диаграммы Венна могут наглядно отображать до 5 наборов данных. Если число превышает это значение, рекомендуется использовать диаграммы UpSet;

Риск искажения площади: площадь круга может быть не пропорциональна размеру набора, а конкретное количество элементов должно быть отмечено на рисунке;

Неприменимо для непрерывных данных: для непрерывных данных, таких как временные ряды, изменения температуры и т. д., необходимо использовать линейную диаграмму или тепловую карту.

От операций с множествами в классе до дифференциального анализа в геномике — диаграмма Венна с ее лаконичным геометрическим языком преобразует абстрактную математическую логику в понятную визуальную модель. По мере увеличения сложности данных комплексное применение диаграмм Венна, диаграмм UpSet, древовидных диаграмм и других инструментов способствует развитию математической визуализации в сторону более высоких измерений. Для учащихся освоение построения и применения диаграмм Венна — это не только овладение инструментом, но и важный способ развития структурированного мышления и навыков междисциплинарного анализа.