Prozess Typ
Grafischer Ausdruck
Denken Typ
Strukturierter Ausdruck
Notizen Typ
Effizienter Ausdruck
Baumkarte
Klammerdiagramm
Standardmodus
Im 19. Jahrhundert erfand der britische Mathematiker John Venn ein Werkzeug zur Darstellung von Mengenbeziehungen mithilfe geometrischer Grafiken – das Venn-Diagramm. Dieser Graphentyp, der überlappende Kreise verwendet, um die Schnittmenge, Vereinigungsmenge und Komplementmenge von Mengen auszudrücken, ist nicht nur zu einem grundlegenden Werkzeug in der Mathematik geworden, sondern hat sich auch als äußerst praktisch in der logischen Argumentation, der Wahrscheinlichkeitsstatistik und der Datenanalyse erwiesen. In diesem Artikel wird der Kernwert des Venn-Diagramms in der Mathematik systematisch anhand von fünf Dimensionen analysiert: Definition, mathematische Anwendungsszenarien, typische Fälle, Produktionswerkzeuge und Zeichenmethoden.
Das Venn-Diagramm stellt die logische Beziehung zwischen mehreren Mengen visuell durch überlappende kreisförmige oder elliptische Bereiche dar. Zu seinen Kernelementen gehören:
Mengendarstellung: Jeder Kreis stellt eine unabhängige Menge dar, und der Bereich innerhalb des Kreises ist das Mengenelement.
Schnittmenge (∩): Der Überlappungsbereich stellt die gemeinsamen Elemente zweier oder mehrerer Mengen dar;
Vereinigung (∪): Die Gesamtfläche, die von allen Kreisen abgedeckt wird, stellt das Ergebnis der Vereinigung der Mengen dar;
Komplement: Der Bereich innerhalb des rechteckigen Kastens (Domäne), der nicht vom Kreis abgedeckt wird, stellt die Elemente dar, die zu keiner Menge gehören.
Beispielsweise stellt im Venn-Diagramm der Gruppe A (Schüler, die Mathematik mögen) und der Gruppe B (Schüler, die Physik mögen) der überlappende Teil „Schüler, die sowohl Mathematik als auch Physik mögen“ dar, und der nicht überlappende Teil stellt „Schüler, die nur Mathematik mögen“ bzw. „Schüler, die nur Physik mögen“ dar.
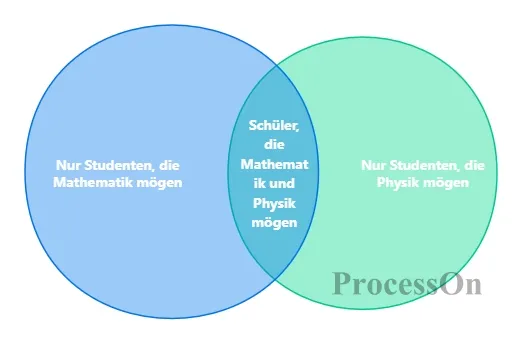
1. Intuitive Mengenoperationen
Venn-Diagramme wandeln abstrakte Mengenoperationen in visuelle Operationen um. Beispielsweise kann beim Beweis des De Morganschen Gesetzes ((A∪B)' = A'∩B') die Gleichheit visuell überprüft werden, indem die Komplementär- und Schnittmenge zweier Mengen dargestellt wird. Diese grafische Beweismethode wird im Mathematikunterricht der Grundschule häufig verwendet, um Schülern dabei zu helfen, die kognitiven Barrieren der symbolischen Logik zu überwinden.
2. Modellierungswerkzeuge für probabilistische Probleme
In der Wahrscheinlichkeitstheorie sind Venn-Diagramme ein leistungsfähiges Werkzeug zum Lösen von Problemen mit unabhängigen Ereignissen, sich gegenseitig ausschließenden Ereignissen und bedingter Wahrscheinlichkeit. Wenn wir beispielsweise die Wahrscheinlichkeit berechnen, „einen Würfel zu werfen und eine gerade Zahl größer als 3 zu erhalten“, können wir den Wahrscheinlichkeitswert des Schnittbereichs {4,6} direkt ermitteln, indem wir ein Venn-Diagramm von Ereignis A (gerade Zahl: {2,4,6}) und Ereignis B (>3: {4,5,6}) zeichnen. Untersuchungen der Universität Cambridge haben gezeigt, dass Studierende, die Venn-Diagramme verwendeten, Wahrscheinlichkeitsprobleme um 40 % effizienter lösen konnten.
3. Der Ableitungsrahmen logischer Aussagen
Venn-Diagramme können logische Aussagen wie „alle A sind B“ und „kein A ist C“ in geometrische Beziehungen umwandeln. Beispielsweise kann in der syllogistischen Argumentation „Alle Metalle sind Leiter, Kupfer ist ein Metall, daher ist Kupfer ein Leiter“ die Notwendigkeit der Schlussfolgerung schnell überprüft werden, indem man einen Kreis der Inklusionsbeziehung zwischen „Metall“ und „Leiter“ zeichnet. Diese Methode des grafischen Denkens wird auch häufig in Bereichen wie der Booleschen Algebra und der Datenbankabfrageoptimierung in der Informatik verwendet.
Statistik zur Kurswahl der Studierenden
Von 50 Schülern einer Klasse entschieden sich 28 für einen Mathematikwettbewerb , 23 für einen Chemiewettbewerb und 5 nahmen an keinem Wettbewerb teil. Durch das Venn-Diagramm lässt sich folgendes Modell erstellen:
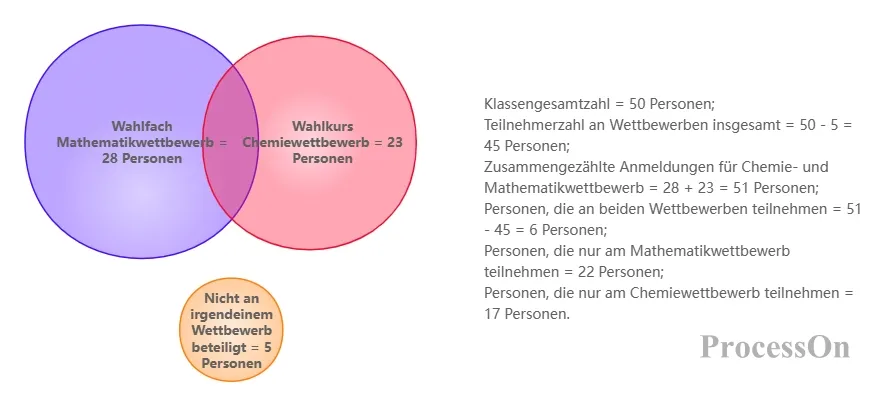
Statistik zur Kurswahl der Studierenden – Venn-Diagramm
Gesamtzahl der Teilnehmer = 50 - 5 = 45;
die Chemie- und Mathematikwettbewerbe = 28 + 23 = 51;
Teilnehmerzahl in beiden Fächern = 51 - 45 = 6.
Das endgültige Venn-Diagramm zeigte: 22 Personen nahmen nur am Mathematikwettbewerb teil , 17 Personen nahmen nur am Wettbewerb teil und 6 Personen nahmen an beiden Fächern teil. Dieser Fall bestätigt die Effizienz des Venn-Diagramms bei der Lösung des „Überlappungszählproblems“.
PPT/SmartArt: Geeignet zum schnellen Zeichnen von Venn-Diagrammen von 2–3 Datensätzen. Über „Einfügen → SmartArt → Beziehung → Einfaches Venn-Diagramm“ können Sie einfache Grafiken erstellen, die die Anpassung von Farbe und Transparenz unterstützen.
Origin/R-Sprache: Beim Umgang mit mehr als drei Sätzen komplexer Daten können das Venn-Diagramm-Plug-In von Origin oder das ggVennDiagram-Paket der R-Sprache hochpräzise Grafiken generieren.
Online-Tool: ProcessOn, bei dem keine Daten eingegeben werden müssen und das das direkte Ziehen von Grafiken auf die Leinwand unterstützt . Es ist für Benutzer ohne Programmierkenntnisse geeignet.
Als nächstes erklären wir am Beispiel von ProcessOn , wie man ein Venn-Diagramm zeichnet:
Definieren Sie einen Satz: Rufen Sie die ProcessOn-Dateiseite auf, erstellen Sie ein neues Flussdiagramm und geben Sie den zu analysierenden Satz an (z. B. Subjekt A, Subjekt B).
Zeichnen Sie Grundformen: Klicken Sie links auf „Weitere Formen“, wählen Sie „Venn-Diagramm“ aus, ziehen Sie zwei Kreise aus dem Formbereich auf die Leinwand und passen Sie die Positionen so an, dass sie sich teilweise überlappen.
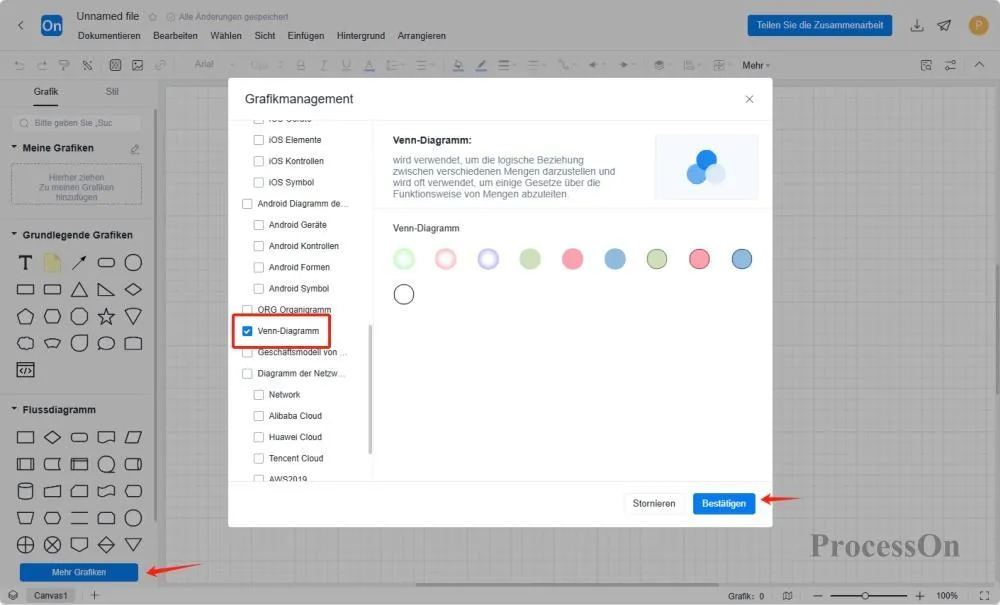
Markierungsbereich: Füllen Sie nicht überlappende Bereiche und Schnittbereiche mit unterschiedlichen Farben und fügen Sie Elementmengenbeschriftungen hinzu.
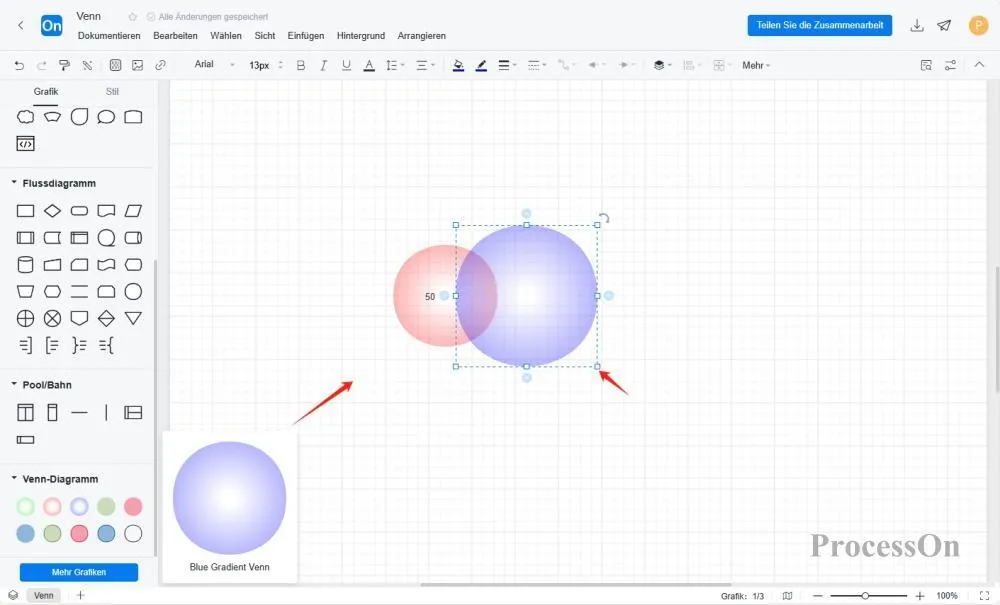
Anzeige optimieren: Farbe, Transparenz usw. anpassen und Textbeschreibungen wie „nur A“, „nur B“, „A∩B“ usw. hinzufügen.
Herunterladen oder teilen: Nachdem Sie das Venn-Diagramm gezeichnet haben, können Sie auf die Schaltfläche „Herunterladen“ in der oberen rechten Ecke klicken, um es in Bilder, PDF und andere Formate zu exportieren oder einen Online-Link zu generieren, um es mit anderen zu teilen.
Obwohl das Venn-Diagramm den Vorteil hat, intuitiv zu sein, sollten auch seine Einschränkungen beachtet werden:
Begrenzung der Anzahl der Sätze: Herkömmliche Venn-Diagramme können bis zu 5 Datensätze übersichtlich darstellen. Wenn die Zahl diesen Wert übersteigt, wird empfohlen, stattdessen UpSet-Diagramme zu verwenden.
Gefahr der Flächenverzerrung: Die Fläche des Kreises ist möglicherweise nicht proportional zur Größe der Menge, und die genaue Anzahl der Elemente muss in der Abbildung markiert werden.
Gilt nicht für kontinuierliche Daten: Für kontinuierliche Daten wie Zeitreihen, Temperaturänderungen usw. müssen Sie stattdessen ein Liniendiagramm oder eine Heatmap verwenden.
Von Mengenoperationen im Klassenzimmer bis hin zur Differenzialanalyse in der Genomik: Das Venn-Diagramm mit seiner prägnanten geometrischen Sprache wandelt abstrakte mathematische Logik in ein wahrnehmbares visuelles Modell um. Angesichts der zunehmenden Datenkomplexität führt die integrierte Anwendung von Venn-Diagrammen, UpSet-Diagrammen, Baumdiagrammen und anderen Tools dazu, dass die mathematische Visualisierung in höhere Dimensionen vordringt. Für Lernende bedeutet das Beherrschen des Zeichnens und der Anwendung von Venn-Diagrammen nicht nur die Beherrschung eines Werkzeugs, sondern auch eine wichtige Möglichkeit, strukturiertes Denken und interdisziplinäre Analysefähigkeiten zu entwickeln.
Kostenloses Online-Mindmap-Flussdiagramm für die Zusammenarbeit
