Processo Tipo
Espressione grafica
Pensiero Tipo
Espressione strutturata
Note Tipo
Espressione efficiente
Mappa ad albero
Diagramma a staffa
Modalità predefinita
Nel XIX secolo, il matematico britannico John Venn inventò uno strumento per visualizzare le relazioni tra insiemi utilizzando grafici geometrici: il diagramma di Venn. Questo tipo di grafico, che utilizza cerchi sovrapposti per esprimere l'intersezione, l'unione e il complemento di insiemi, non solo è diventato uno strumento fondamentale nel campo della matematica, ma ha anche dimostrato una notevole praticità nel ragionamento logico, nelle statistiche sulle probabilità e nell'analisi dei dati. Questo articolo analizzerà sistematicamente il valore fondamentale del diagramma di Venn in matematica partendo da cinque dimensioni: definizione, scenari di applicazione matematica, casi tipici, strumenti di produzione e metodi di disegno.
Il diagramma di Venn presenta visivamente la relazione logica tra più insiemi attraverso aree circolari o ellittiche sovrapposte. I suoi elementi principali includono:
Rappresentazione dell'insieme: ogni cerchio rappresenta un insieme indipendente e l'area all'interno del cerchio è l'elemento dell'insieme;
Intersezione (∩): l'area di sovrapposizione rappresenta gli elementi comuni di due o più insiemi;
Unione (∪): L'area totale coperta da tutti i cerchi rappresenta il risultato dell'unione degli insiemi;
Complemento: l'area all'interno del riquadro rettangolare (dominio) non coperta dal cerchio rappresenta gli elementi che non appartengono a nessun insieme.
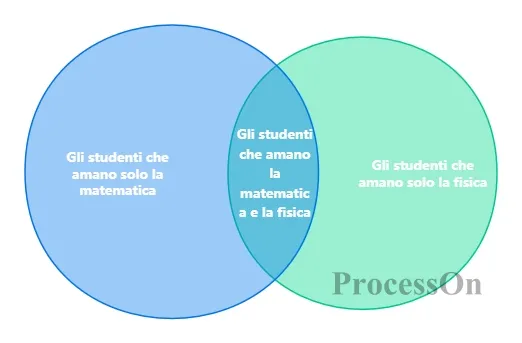
Ad esempio, nel diagramma di Venn dell'insieme A (studenti a cui piace la matematica) e dell'insieme B (studenti a cui piace la fisica), la parte sovrapposta rappresenta "studenti a cui piacciono sia la matematica che la fisica", mentre la parte non sovrapposta rappresenta rispettivamente "studenti a cui piace solo la matematica" e "studenti a cui piace solo la fisica".
1. Operazioni intuitive sugli insiemi
I diagrammi di Venn trasformano le operazioni astratte sugli insiemi in operazioni visive. Ad esempio, quando si dimostra la legge di De Morgan ((A∪B)' = A'∩B'), l'uguaglianza può essere verificata visivamente tracciando il complemento e l'intersezione di due insiemi. Questo metodo di dimostrazione grafica è ampiamente utilizzato nell'insegnamento della matematica elementare per aiutare gli studenti a superare le barriere cognitive della logica simbolica.
2. Strumenti di modellazione per problemi probabilistici
Nella teoria della probabilità, i diagrammi di Venn sono uno strumento potente per risolvere problemi di eventi indipendenti, eventi mutuamente esclusivi e probabilità condizionata. Ad esempio, quando calcoliamo la probabilità di "lanciare un dado e ottenere un numero pari maggiore di 3", possiamo ottenere direttamente il valore di probabilità dell'area di intersezione {4,6} disegnando un diagramma di Venn dell'evento A (numero pari: {2,4,6}) e dell'evento B (>3: {4,5,6}). Una ricerca dell'Università di Cambridge ha dimostrato che gli studenti che utilizzavano i diagrammi di Venn erano il 40% più efficienti nel risolvere problemi di probabilità.
3. Il quadro di derivazione delle proposizioni logiche
I diagrammi di Venn possono trasformare proposizioni logiche come "tutti gli A sono B" e "nessun A è C" in relazioni geometriche. Ad esempio, nel ragionamento sillogistico "tutti i metalli sono conduttori, il rame è un metallo, quindi il rame è un conduttore", tracciando un cerchio di relazione di inclusione tra "metallo" e "conduttore", si può rapidamente verificare la necessità della conclusione. Questo metodo di ragionamento grafico è ampiamente utilizzato anche in campi quali l'algebra booleana e l'ottimizzazione delle query dei database nell'informatica.
Statistiche sulla selezione dei corsi da parte degli studenti
Tra i 50 studenti di una classe, 28 hanno scelto la gara di matematica , 23 hanno scelto la gara di chimica e 5 non hanno partecipato ad alcuna gara. Attraverso il diagramma di Venn è possibile stabilire il seguente modello:
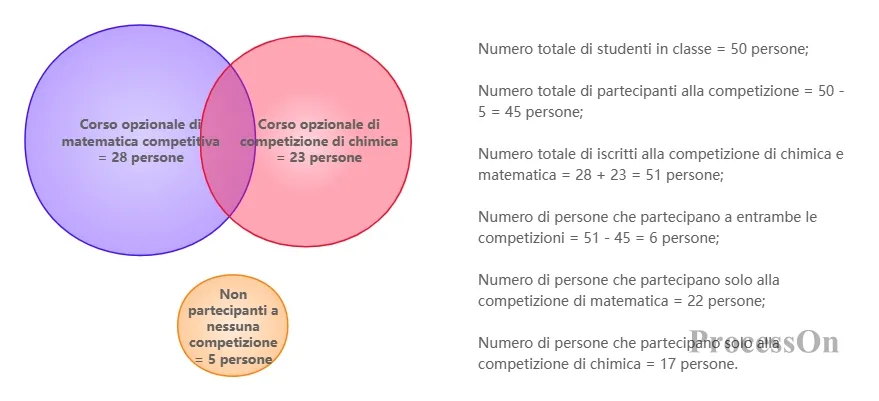
Statistiche sulla selezione dei corsi da parte degli studenti - Diagramma di Venn
Numero totale dei partecipanti = 50 - 5 = 45;
i concorsi di Chimica e Matematica = 28 + 23 = 51;
Numero di partecipanti in entrambe le materie = 51 - 45 = 6.
Il diagramma di Venn finale mostrava: 22 persone hanno partecipato solo alla gara di matematica , 17 persone hanno partecipato solo alla gara e 6 persone hanno partecipato a entrambe le materie. Questo caso verifica l'efficienza del diagramma di Venn nel risolvere il "problema del conteggio sovrapposto".
PPT/SmartArt: adatto per disegnare rapidamente diagrammi di Venn di 2-3 set di dati. È possibile generare grafici di base tramite "Inserisci → SmartArt → Relazione → Diagramma di Venn di base", che supporta la regolazione del colore e della trasparenza.
Linguaggio Origin/R: quando si ha a che fare con più di tre set di dati complessi, il plug-in del diagramma di Venn di Origin o il pacchetto ggVennDiagram del linguaggio R possono generare grafici ad alta precisione.
Strumento online: ProcessOn, che non richiede l'inserimento di dati e supporta il trascinamento diretto della grafica sulla tela . È adatto agli utenti senza conoscenze di programmazione.
Successivamente , prendendo ProcessOn come esempio , spiegheremo come disegnare un diagramma di Venn:
Definisci un set: accedi alla pagina del file ProcessOn, crea un nuovo diagramma di flusso e specifica il set da analizzare (ad esempio soggetto A, soggetto B);
Disegna forme di base: fai clic su "Altre forme" a sinistra, seleziona il diagramma di Venn, trascina due cerchi dall'area della forma alla tela e regola le posizioni in modo che si sovrappongano parzialmente;
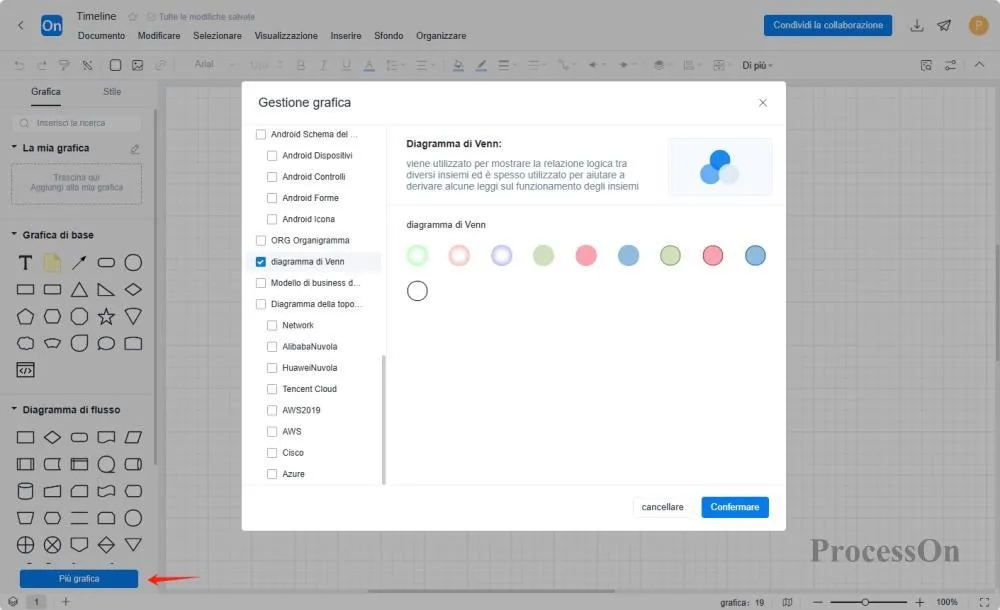
Area di marcatura: riempire le aree non sovrapposte e le aree di intersezione con colori diversi e aggiungere etichette per la quantità degli elementi;
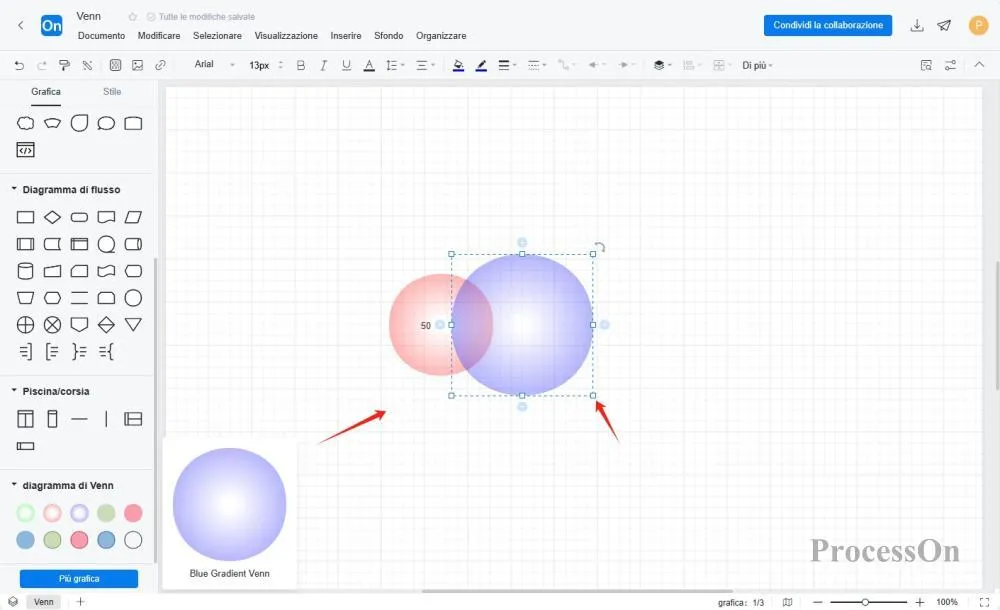
Ottimizza la visualizzazione: regola il colore, la trasparenza , ecc . e aggiungi descrizioni di testo come "solo A", "solo B", "A∩B", ecc.
Scarica o condividi: dopo aver disegnato il diagramma di Venn, puoi cliccare sul pulsante di download nell'angolo in alto a destra per esportarlo in formato immagine, PDF o altri formati, oppure generare un collegamento online da condividere con altri.
Sebbene il diagramma di Venn abbia il vantaggio di essere intuitivo, è opportuno notare anche i suoi limiti:
Limitazione del numero di set: i diagrammi di Venn tradizionali possono visualizzare chiaramente fino a 5 set di dati. Se il numero supera questo valore, si consiglia di utilizzare invece i diagrammi UpSet;
Rischio di distorsione dell'area: l'area del cerchio potrebbe non essere proporzionale alla dimensione dell'insieme e il numero specifico di elementi deve essere contrassegnato nella figura;
Non applicabile ai dati continui: per dati continui quali serie temporali, variazioni di temperatura, ecc., è necessario utilizzare invece un grafico a linee o una mappa termica.
Dalle operazioni sugli insiemi in classe all'analisi differenziale in genomica, il diagramma di Venn, con il suo linguaggio geometrico conciso, trasforma la logica matematica astratta in un modello visivo percepibile. Con l'aumento della complessità dei dati, l'applicazione integrata di diagrammi di Venn, diagrammi UpSet, diagrammi ad albero e altri strumenti sta spingendo la visualizzazione matematica a evolversi verso dimensioni più elevate. Per gli studenti, padroneggiare il disegno e l'applicazione dei diagrammi di Venn non significa solo padroneggiare uno strumento, ma anche un modo importante per coltivare il pensiero strutturato e le capacità di analisi interdisciplinare.
Diagramma di flusso della mappa mentale collaborativa online gratuita
