Processo Tipo
Expressão gráfica
Pensamento Tipo
Expressão estruturada
Anotações Tipo
Expressão eficiente
Mapa de árvore
Diagrama de colchetes
Modo padrão
No século XIX, o matemático britânico John Venn inventou uma ferramenta para exibir relações de conjuntos usando gráficos geométricos: o Diagrama de Venn. Esse tipo de gráfico, que usa círculos sobrepostos para expressar a interseção, união e complemento de conjuntos, não se tornou apenas uma ferramenta básica no campo da matemática, mas também demonstrou grande praticidade no raciocínio lógico, nas estatísticas de probabilidade e na análise de dados. Este artigo analisará sistematicamente o valor central do diagrama de Venn na matemática a partir de cinco dimensões: definição, cenários de aplicação matemática, casos típicos, ferramentas de produção e métodos de desenho.
O diagrama de Venn apresenta visualmente a relação lógica entre vários conjuntos por meio de áreas circulares ou elípticas sobrepostas. Seus principais elementos incluem:
Representação do conjunto: Cada círculo representa um conjunto independente, e a área dentro do círculo é o elemento do conjunto;
Intersecção (∩): A área de sobreposição representa os elementos comuns de dois ou mais conjuntos;
União (∪): A área total coberta por todos os círculos representa o resultado da união dos conjuntos;
Complemento: A área dentro da caixa retangular (domínio) não coberta pelo círculo representa os elementos que não pertencem a nenhum conjunto.
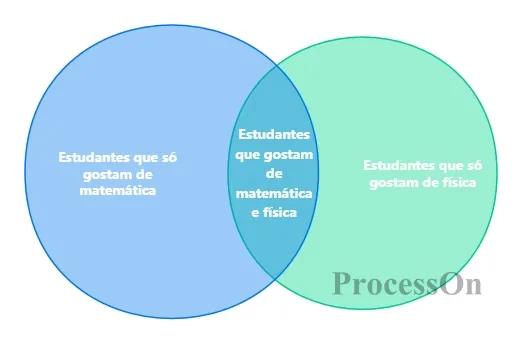
Por exemplo, no diagrama de Venn do conjunto A (alunos que gostam de matemática) e do conjunto B (alunos que gostam de física), a parte sobreposta representa "alunos que gostam de matemática e física", e a parte não sobreposta representa "alunos que gostam apenas de matemática" e "alunos que gostam apenas de física", respectivamente.
1. Operações de conjunto intuitivas
Os diagramas de Venn transformam operações de conjuntos abstratos em operações visuais. Por exemplo, ao provar a lei de De Morgan ((A∪B)' = A'∩B'), a igualdade pode ser verificada visualmente plotando o complemento e a interseção de dois conjuntos. Este método de prova gráfica é amplamente utilizado no ensino de matemática elementar para ajudar os alunos a quebrar as barreiras cognitivas da lógica simbólica.
2. Ferramentas de modelagem para problemas probabilísticos
Na teoria da probabilidade, os diagramas de Venn são uma ferramenta poderosa para resolver problemas de eventos independentes, eventos mutuamente exclusivos e probabilidade condicional. Por exemplo, ao calcular a probabilidade de "rolar um dado e obter um número par maior que 3", podemos obter diretamente o valor de probabilidade da área de interseção {4,6} desenhando um diagrama de Venn do evento A (número par: {2,4,6}) e do evento B (>3: {4,5,6}). Uma pesquisa da Universidade de Cambridge mostrou que alunos que usaram diagramas de Venn foram 40% mais eficientes na resolução de problemas de probabilidade.
3. A estrutura de derivação de proposições lógicas
Os diagramas de Venn podem transformar proposições lógicas como "todos os A são B" e "nenhum A é C" em relações geométricas. Por exemplo, no raciocínio silogístico "todos os metais são condutores, o cobre é um metal, portanto o cobre é um condutor", ao traçar um círculo de relação de inclusão entre "metal" e "condutor", a necessidade da conclusão pode ser rapidamente verificada. Este método de raciocínio gráfico também é amplamente utilizado em áreas como álgebra booleana e otimização de consultas de banco de dados em ciência da computação.
Estatísticas de seleção de cursos de alunos
Entre 50 alunos de uma turma, 28 escolheram competição de matemática , 23 escolheram competição de química e 5 não participaram de nenhuma competição. O seguinte modelo pode ser estabelecido através do diagrama de Venn:
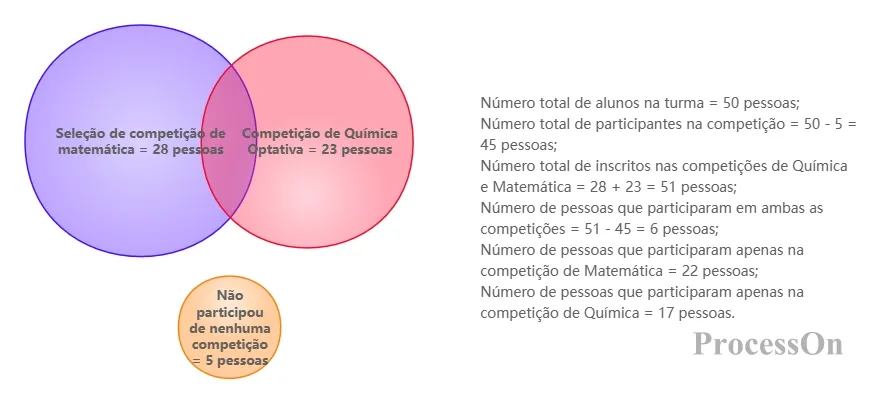
Estatísticas de seleção de cursos por alunos - diagrama de Venn
Número total de participantes = 50 - 5 = 45;
Química e Matemática = 28 + 23 = 51;
Número de participantes em ambas as disciplinas = 51 - 45 = 6.
O diagrama de Venn final mostrou: 22 pessoas participaram apenas da competição de matemática , 17 pessoas participaram apenas da competição e 6 pessoas participaram de ambas as disciplinas. Este caso verifica a eficiência do diagrama de Venn na resolução do "problema de contagem de sobreposição".
PPT/SmartArt: Adequado para desenhar rapidamente diagramas de Venn de 2 a 3 conjuntos de dados. Você pode gerar gráficos básicos por meio de "Inserir → SmartArt → Relacionamento → Diagrama de Venn básico", que suporta ajustes de cor e transparência.
Linguagem Origin/R: Ao lidar com mais de três conjuntos de dados complexos, o plug-in Venn Diagram da Origin ou o pacote ggVennDiagram da linguagem R podem gerar gráficos de alta precisão.
Ferramenta on-line: ProcessOn, que não exige preenchimento de dados e permite arrastar gráficos diretamente para a tela . É adequado para usuários sem conhecimento de programação.
A seguir , tomando o ProcessOn como exemplo , apresentaremos como desenhar um diagrama de Venn:
Definir um conjunto: Entre na página do arquivo ProcessOn, crie um novo fluxograma e especifique o conjunto a ser analisado (como assunto A, assunto B);
Desenhe formas básicas: clique em "Mais formas" à esquerda, selecione o diagrama de Venn, arraste dois círculos da área de formas para a tela e ajuste as posições para que elas se sobreponham parcialmente;
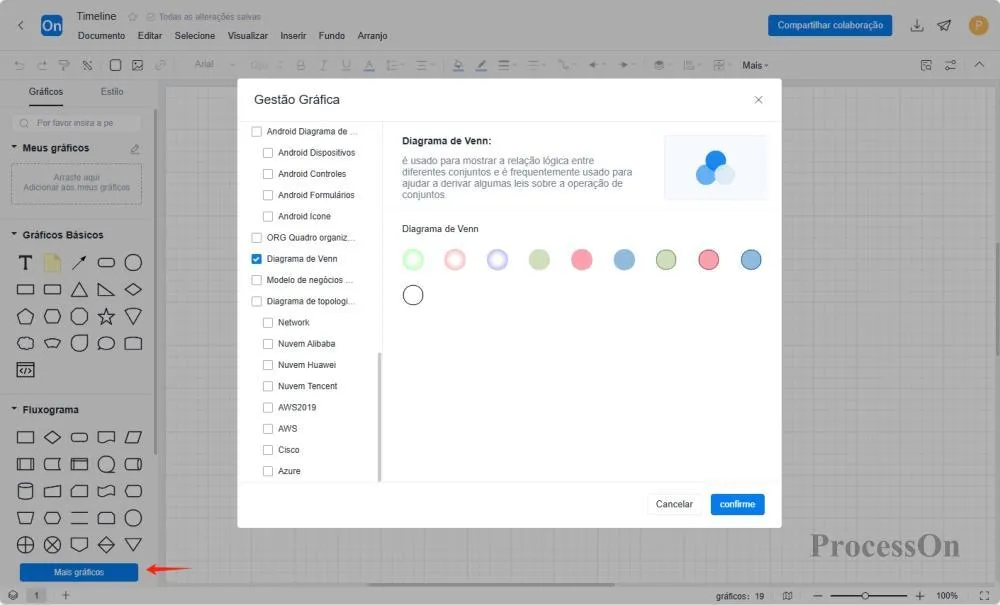
Área de marcação: preencha áreas não sobrepostas e áreas de intersecção com cores diferentes e adicione rótulos de quantidade de elementos;
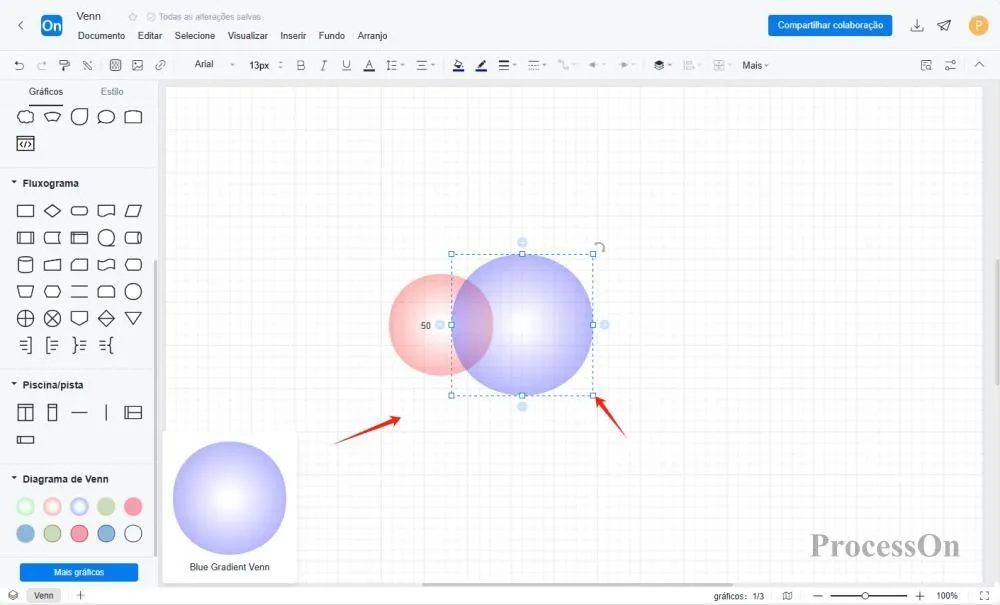
Otimize a exibição: ajuste a cor, a transparência , etc. , e adicione descrições de texto como "somente A", "somente B", "A∩B", etc.
Baixar ou compartilhar: depois de desenhar o diagrama de Venn, você pode clicar no botão de download no canto superior direito para exportá-lo para imagem, PDF ou outros formatos, ou gerar um link on-line para compartilhar com outras pessoas.
Embora o diagrama de Venn tenha a vantagem de ser intuitivo, suas limitações também devem ser observadas:
Limitação no número de conjuntos: os diagramas de Venn tradicionais podem exibir claramente até 5 conjuntos de dados. Se o número exceder esse valor, é recomendável usar diagramas UpSet;
Risco de distorção da área: A área do círculo pode não ser proporcional ao tamanho do conjunto, sendo necessário marcar na figura o número específico de elementos;
Não aplicável para dados contínuos: para dados contínuos, como séries temporais, mudanças de temperatura, etc., você precisa usar um gráfico de linhas ou um mapa de calor.
Das operações definidas na sala de aula à análise diferencial em genômica, o diagrama de Venn, com sua linguagem geométrica concisa, transforma a lógica matemática abstrata em um modelo visual perceptível. À medida que a complexidade dos dados aumenta, a aplicação integrada de diagramas de Venn, diagramas UpSet, diagramas de árvore e outras ferramentas está levando a visualização matemática a evoluir para dimensões mais altas. Para os alunos, dominar o desenho e a aplicação de diagramas de Venn não significa apenas dominar uma ferramenta, mas também uma maneira importante de cultivar o pensamento estruturado e as capacidades de análise interdisciplinar.
Fluxograma de mapa mental colaborativo online gratuito
