19세기에 영국의 수학자 존 벤은 기하학적 그래픽을 사용하여 집합 관계를 표시하는 도구인 벤 다이어그램을 발명했습니다. 교집합, 합집합, 보수를 표현하기 위해 겹치는 원을 사용하는 이러한 유형의 그래프는 수학 분야의 기본 도구가 되었을 뿐만 아니라 논리적 추론, 확률 통계, 데이터 분석에서도 강력한 실용성을 보여주었습니다. 이 글에서는 수학에서 벤 다이어그램의 핵심 가치를 정의, 수학적 응용 시나리오, 일반적인 사례, 생산 도구 및 도면 방법의 5가지 측면에서 체계적으로 분석합니다.
벤 다이어그램은 여러 집합 간의 논리적 관계를 겹쳐진 원형 또는 타원형 영역을 통해 시각적으로 표현합니다. 핵심 요소는 다음과 같습니다.
집합 표현: 각 원은 독립적인 집합을 나타내며, 원 안의 면적은 집합의 원소입니다.
교집합(∩): 겹치는 영역은 두 개 이상의 집합의 공통 요소를 나타냅니다.
합집합(∪): 모든 원으로 덮인 총 면적은 집합의 합집합의 결과를 나타냅니다.
여집합: 원으로 덮이지 않은 직사각형 상자(도메인) 내의 영역은 어떤 집합에도 속하지 않는 원소를 나타냅니다.
예를 들어, 집합 A(수학을 좋아하는 학생)와 집합 B(물리학을 좋아하는 학생)의 벤 다이어그램에서 겹치는 부분은 "수학과 물리를 모두 좋아하는 학생"을 나타내고, 겹치지 않는 부분은 각각 "수학만 좋아하는 학생"과 "물리학만 좋아하는 학생"을 나타냅니다.
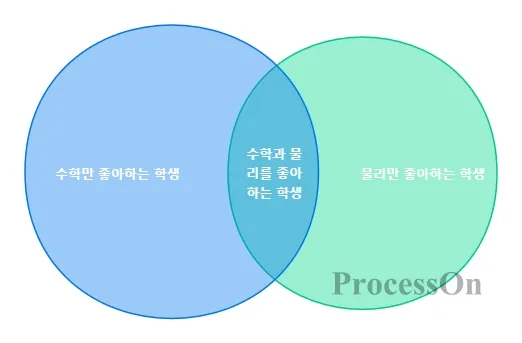
1. 직관적인 집합 연산
벤 다이어그램은 추상적인 집합 연산을 시각적 연산으로 변환합니다. 예를 들어, 드 모르간의 법칙((A∪B)' = A'∩B')을 증명할 때, 두 집합의 여집합과 교집합을 그려서 동일성을 시각적으로 확인할 수 있습니다. 이러한 그래픽 증명 방법은 초등 수학 교육에서 학생들이 기호 논리의 인지적 장벽을 돌파하는 데 도움이 되도록 널리 사용됩니다.
2. 확률 문제를 위한 모델링 도구
확률론에서 벤 다이어그램은 독립 사건, 상호 배타적 사건, 조건부 확률 문제를 해결하는 강력한 도구입니다. 예를 들어, "주사위를 굴려서 3보다 큰 짝수가 나올" 확률을 계산할 때, 사건 A(짝수: {2,4,6})와 사건 B(3보다 큰 수: {4,5,6})에 대한 벤 다이어그램을 그리면 교차 영역 {4,6}의 확률 값을 직접 얻을 수 있습니다. 케임브리지 대학의 연구에 따르면 벤 다이어그램을 사용한 학생들은 확률 문제를 푸는 효율성이 40% 더 높은 것으로 나타났습니다.
3. 논리적 명제의 도출 프레임워크
벤 다이어그램은 "모든 A는 B이다", "어떤 A도 C가 아니다"와 같은 논리적 명제를 기하학적 관계로 변환할 수 있습니다. 예를 들어, "모든 금속은 도체이고, 구리는 금속이므로 구리는 도체이다"라는 삼단논법적 추론에서 "금속"과 "도체" 사이에 포함 관계의 원을 그리면 결론의 필연성을 빠르게 검증할 수 있습니다. 이러한 그래픽 추론 방법은 컴퓨터 과학의 부울 대수와 데이터베이스 쿼리 최적화와 같은 분야에서도 널리 사용됩니다.
학생 과목 선택 통계
한 학급의 학생 50명 중 28명은 수학 경시 대회를 선택했고, 23명은 화학 경시 대회를 선택했으며, 5명은 어떤 경시대회에도 참여하지 않았습니다. 다음 모델은 벤 다이어그램을 통해 확립될 수 있습니다.
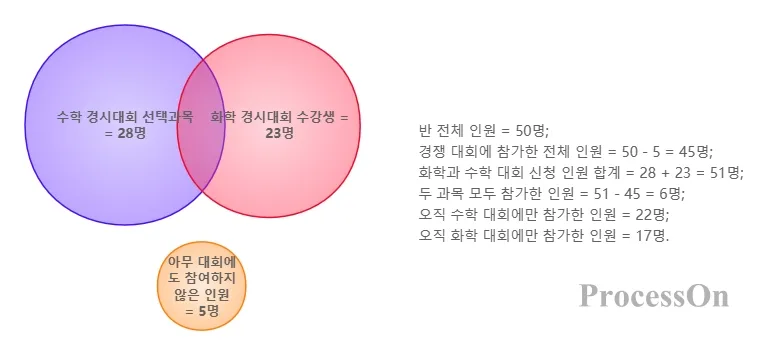
참가자 총 수 = 50 - 5 = 45;
화학과 수학 경시대회에 지원한 사람의 수의 합은 28 + 23 = 51입니다.
두 과목의 참여자 수 = 51 - 45 = 6.
최종 벤 다이어그램은 다음과 같습니다. 22명이 수학 경시 대회에만 참여했고, 17명이 경시대회에만 참여했으며, 6명이 두 과목 모두에 참여했습니다. 이 사례는 "중복 계산 문제"를 해결하는 데 있어서 벤 다이어그램의 효율성을 검증합니다.
PPT/SmartArt: 2~3개 데이터 세트의 벤 다이어그램을 빠르게 그리는 데 적합합니다. "삽입 → SmartArt → 관계 → 기본 벤 다이어그램"을 통해 색상 및 투명도 조정을 지원하여 기본적인 그래픽을 생성할 수 있습니다.
Origin/R 언어: 세 개 이상의 복잡한 데이터 세트를 다루는 경우 Origin의 벤 다이어그램 플러그인이나 R 언어의 ggVennDiagram 패키지를 사용하여 고정밀 그래픽을 생성할 수 있습니다.
온라인 도구: ProcessOn은 데이터를 입력할 필요가 없고 캔버스에 그래픽을 직접 끌어다 놓을 수 있는 기능 을 지원합니다 . 프로그래밍 지식이 없는 사용자에게 적합합니다.
다음으로 ProcessOn을 예로 들어 벤 다이어그램을 그리는 방법을 소개합니다 .
세트 정의: ProcessOn 파일 페이지로 들어가서 새로운 흐름도를 만들고 분석할 세트를 지정합니다(예: 주제 A, 주제 B).
기본 도형 그리기: 왼쪽의 "다른 도형"을 클릭하고 벤 다이어그램을 선택한 다음 도형 영역에서 두 개의 원을 캔버스로 끌어다 놓고 두 원이 부분적으로 겹치도록 위치를 조정합니다.
표시 영역: 겹치지 않는 영역과 교차 영역을 다양한 색상으로 채우고, 요소 수량 라벨을 추가합니다.
디스플레이 최적화: 색상, 투명도 등 을 조정하고 "A만", "B만", "A∩B" 등과 같은 텍스트 설명을 추가합니다.
다운로드 또는 공유: 벤 다이어그램을 그린 후 오른쪽 상단의 다운로드 버튼을 클릭하여 이미지, PDF 또는 기타 형식으로 내보내거나 온라인 링크를 생성하여 다른 사람들과 공유할 수 있습니다.
벤 다이어그램은 직관적이라는 장점이 있지만, 한계점도 주의해야 합니다.
세트 수 제한: 기존 벤 다이어그램은 최대 5개 세트의 데이터를 명확하게 표시할 수 있습니다. 숫자가 이를 초과하면 대신 UpSet 다이어그램을 사용하는 것이 좋습니다.
면적 왜곡의 위험: 원의 면적은 집합의 크기에 비례하지 않을 수 있으며, 그림에서 구체적인 요소 수를 표시해야 합니다.
연속형 데이터에는 적용할 수 없습니다. 시계열, 온도 변화 등과 같은 연속형 데이터의 경우 대신 선형 차트나 히트맵을 사용해야 합니다.
교실에서의 집합 연산부터 유전체학에서의 미분 분석까지, 간결한 기하학적 언어로 표현된 벤 다이어그램은 추상적인 수학적 논리를 인지 가능한 시각적 모델로 변환합니다. 데이터의 복잡성이 증가함에 따라 벤 다이어그램, 업셋 다이어그램, 트리 다이어그램 및 기타 도구를 통합적으로 적용하여 수학적 시각화가 더 높은 차원으로 발전하고 있습니다. 학습자에게 벤 다이어그램을 그리고 적용하는 법을 익히는 것은 단순히 도구를 익히는 것만이 아니라, 체계적인 사고와 학제간 분석 능력을 기르는 중요한 방법입니다.