Proceso Tipo
Expresión gráfica
Pensamiento Tipo
Expresión estructurada
Notas Tipo
Expresión eficiente
Mapa de árbol
Diagrama de soportes
Modo predeterminado
En el siglo XIX, el matemático británico John Venn inventó una herramienta para mostrar relaciones entre conjuntos utilizando gráficos geométricos: el diagrama de Venn. Este tipo de gráfico, que utiliza círculos superpuestos para expresar la intersección, unión y complemento de conjuntos, no sólo se ha convertido en una herramienta básica en el campo de las matemáticas, sino que también ha demostrado una poderosa practicidad en el razonamiento lógico, la estadística de probabilidad y el análisis de datos. Este artículo analizará sistemáticamente el valor central del diagrama de Venn en matemáticas desde cinco dimensiones: definición, escenarios de aplicación matemática, casos típicos, herramientas de producción y métodos de dibujo.
El diagrama de Venn presenta visualmente la relación lógica entre múltiples conjuntos a través de áreas circulares o elípticas superpuestas. Sus elementos principales incluyen:
Representación del conjunto: cada círculo representa un conjunto independiente y el área dentro del círculo es el elemento del conjunto;
Intersección (∩): El área superpuesta representa los elementos comunes de dos o más conjuntos;
Unión (∪): El área total cubierta por todos los círculos representa el resultado de la unión de los conjuntos;
Complemento: El área dentro del cuadro rectangular (dominio) no cubierta por el círculo representa los elementos que no pertenecen a ningún conjunto.
Por ejemplo, en el diagrama de Venn del conjunto A (estudiantes a los que les gustan las matemáticas) y el conjunto B (estudiantes a los que les gusta la física), la parte superpuesta representa a los "estudiantes a los que les gustan tanto las matemáticas como la física", y la parte no superpuesta representa a los "estudiantes a los que solo les gustan las matemáticas" y a los "estudiantes a los que solo les gusta la física", respectivamente.
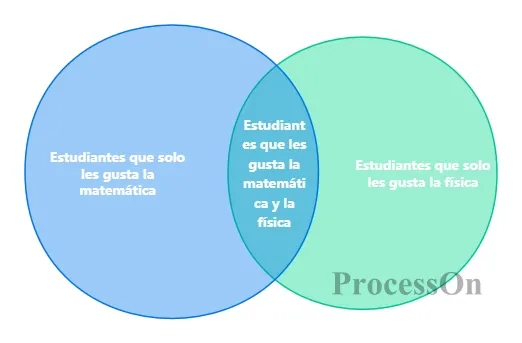
1. Operaciones intuitivas con conjuntos
Los diagramas de Venn transforman operaciones de conjuntos abstractos en operaciones visuales. Por ejemplo, al probar la ley de De Morgan ((A∪B)' = A'∩B'), la igualdad se puede verificar visualmente trazando el complemento y la intersección de dos conjuntos. Este método de prueba gráfica se utiliza ampliamente en la educación matemática elemental para ayudar a los estudiantes a romper las barreras cognitivas de la lógica simbólica.
2. Herramientas de modelado para problemas probabilísticos
En la teoría de la probabilidad, los diagramas de Venn son una herramienta poderosa para resolver problemas de eventos independientes, eventos mutuamente excluyentes y probabilidad condicional. Por ejemplo, al calcular la probabilidad de "lanzar un dado y obtener un número par mayor que 3", podemos obtener directamente el valor de probabilidad del área de intersección {4,6} dibujando un diagrama de Venn del evento A (número par: {2,4,6}) y el evento B (>3: {4,5,6}). Una investigación de la Universidad de Cambridge demostró que los estudiantes que utilizaban diagramas de Venn eran un 40% más eficientes al resolver problemas de probabilidad.
3. El marco de derivación de proposiciones lógicas
Los diagramas de Venn pueden transformar proposiciones lógicas como "todos los A son B" y "ningún A es C" en relaciones geométricas. Por ejemplo, en el razonamiento silogístico "todos los metales son conductores, el cobre es un metal, por lo tanto el cobre es un conductor", al trazar un círculo de relación de inclusión entre "metal" y "conductor", se puede verificar rápidamente la necesidad de la conclusión. Este método de razonamiento gráfico también se utiliza ampliamente en campos como el álgebra booleana y la optimización de consultas de bases de datos en informática.
Estadísticas de selección de cursos por parte de los estudiantes
Entre 50 estudiantes de una clase, 28 eligieron la competencia de matemáticas , 23 eligieron la competencia de química y 5 no participaron en ninguna competencia. A través del diagrama de Venn se puede establecer el siguiente modelo:
Estadísticas de selección de cursos por parte de estudiantes : diagrama de Venn
Número total de participantes = 50 - 5 = 45;
los concursos de Química y Matemáticas = 28 + 23 = 51;
Número de participantes en ambas asignaturas = 51 – 45 = 6.
El diagrama de Venn final mostró: 22 personas participaron solo en la competencia de matemáticas , 17 personas participaron solo en la competencia y 6 personas participaron en ambas materias. Este caso verifica la eficiencia del diagrama de Venn para resolver el "problema de conteo superpuesto".
PPT/SmartArt: adecuado para dibujar rápidamente diagramas de Venn de 2 a 3 conjuntos de datos. Puede generar gráficos básicos a través de "Insertar → SmartArt → Relación → Diagrama de Venn básico", que admite el ajuste de color y transparencia.
Lenguaje Origin/R: Al trabajar con más de tres conjuntos de datos complejos, el complemento Diagrama de Venn de Origin o el paquete ggVennDiagram del lenguaje R pueden generar gráficos de alta precisión.
Herramienta en línea: ProcessOn, que no requiere que se rellenen datos y admite arrastrar gráficos directamente al lienzo . Es adecuado para usuarios sin conocimientos de programación.
A continuación , tomando ProcessOn como ejemplo , presentaremos cómo dibujar un diagrama de Venn:
Definir un conjunto: Ingrese a la página del archivo ProcessOn, cree un nuevo diagrama de flujo y especifique el conjunto que se analizará (por ejemplo, sujeto A, sujeto B);
Dibujar formas básicas: haga clic en "Más formas" a la izquierda, seleccione el diagrama de Venn, arrastre dos círculos desde el área de forma al lienzo y ajuste las posiciones para que se superpongan parcialmente;
Área de marcado: rellene las áreas no superpuestas y las áreas de intersección con diferentes colores y agregue etiquetas de cantidad de elementos;
Optimizar la visualización: ajustar el color, la transparencia , etc. , y agregar descripciones de texto como "solo A", "solo B", "A∩B", etc.
Descargar o compartir: Después de dibujar el diagrama de Venn, puede hacer clic en el botón de descarga en la esquina superior derecha para exportarlo a imagen, PDF u otros formatos, o generar un enlace en línea para compartir con otros.
VI. Limitaciones de los diagramas de Venn
Aunque el diagrama de Venn tiene la ventaja de ser intuitivo, también deben tenerse en cuenta sus limitaciones:
Limitación en el número de conjuntos: los diagramas de Venn tradicionales pueden mostrar claramente hasta 5 conjuntos de datos. Si el número excede este, se recomienda utilizar diagramas UpSet en su lugar;
Riesgo de distorsión del área: el área del círculo puede no ser proporcional al tamaño del conjunto y es necesario marcar el número específico de elementos en la figura;
No aplicable para datos continuos: para datos continuos, como series de tiempo, cambios de temperatura, etc., es necesario utilizar un gráfico de líneas o un mapa de calor.
Desde las operaciones con conjuntos en el aula hasta el análisis diferencial en genómica, el diagrama de Venn, con su lenguaje geométrico conciso, transforma la lógica matemática abstracta en un modelo visual perceptible. A medida que aumenta la complejidad de los datos, la aplicación integrada de diagramas de Venn, diagramas UpSet, diagramas de árbol y otras herramientas está impulsando la visualización matemática a evolucionar hacia dimensiones superiores. Para los estudiantes, dominar el dibujo y la aplicación de diagramas de Venn no se trata solo de dominar una herramienta, sino también de una forma importante de cultivar el pensamiento estructurado y las capacidades de análisis interdisciplinario.
Diagrama de flujo de mapas mentales colaborativos en línea gratuito
