Type de processus
Expression graphique
Type de réflexion
Expression structurée
Type de note
Expression efficace
Carte arborescente
Diagramme de parenthèses
Mode par défaut
Au XIXe siècle, le mathématicien britannique John Venn a inventé un outil permettant d'afficher les relations entre les ensembles à l'aide de graphiques géométriques : le diagramme de Venn. Ce type de graphique, qui utilise des cercles superposés pour exprimer l'intersection, l'union et le complément d'ensembles, est non seulement devenu un outil de base dans le domaine des mathématiques, mais a également démontré une grande praticité dans le raisonnement logique, les statistiques de probabilité et l'analyse de données. Cet article analysera systématiquement la valeur fondamentale du diagramme de Venn en mathématiques à partir de cinq dimensions : définition, scénarios d'application mathématique, cas typiques, outils de production et méthodes de dessin.
Le diagramme de Venn présente visuellement la relation logique entre plusieurs ensembles à travers des zones circulaires ou elliptiques qui se chevauchent. Ses éléments principaux comprennent :
Représentation d'ensemble : Chaque cercle représente un ensemble indépendant, et la zone à l'intérieur du cercle est l'élément de l'ensemble ;
Intersection (∩) : La zone de chevauchement représente les éléments communs de deux ou plusieurs ensembles ;
Union (∪) : L'aire totale couverte par tous les cercles représente le résultat de l'union des ensembles ;
Complément : La zone à l'intérieur de la boîte rectangulaire (domaine) non couverte par le cercle représente les éléments qui n'appartiennent à aucun ensemble.
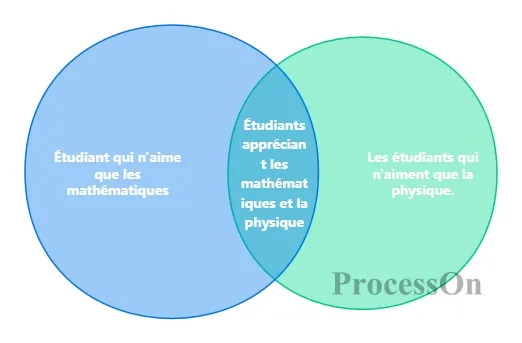
Par exemple, dans le diagramme de Venn de l'ensemble A (étudiants qui aiment les mathématiques) et de l'ensemble B (étudiants qui aiment la physique), la partie qui se chevauche représente « les étudiants qui aiment à la fois les mathématiques et la physique », et la partie qui ne se chevauche pas représente respectivement « les étudiants qui aiment seulement les mathématiques » et « les étudiants qui aiment seulement la physique ».
1. Opérations d'ensemble intuitives
Les diagrammes de Venn transforment les opérations d’ensemble abstraites en opérations visuelles. Par exemple, lors de la preuve de la loi de De Morgan ((A∪B)' = A'∩B'), l'égalité peut être vérifiée visuellement en traçant le complément et l'intersection de deux ensembles. Cette méthode de preuve graphique est largement utilisée dans l’enseignement des mathématiques élémentaires pour aider les élèves à franchir les barrières cognitives de la logique symbolique.
2. Outils de modélisation pour les problèmes probabilistes
En théorie des probabilités, les diagrammes de Venn sont un outil puissant pour résoudre les problèmes d’événements indépendants, d’événements mutuellement exclusifs et de probabilité conditionnelle. Par exemple, lors du calcul de la probabilité de « lancer un dé et d'obtenir un nombre pair supérieur à 3 », nous pouvons obtenir directement la valeur de probabilité de la zone d'intersection {4,6} en dessinant un diagramme de Venn de l'événement A (nombre pair : {2,4,6}) et de l'événement B (>3 : {4,5,6}). Des recherches menées à l’Université de Cambridge ont montré que les étudiants qui utilisaient des diagrammes de Venn étaient 40 % plus efficaces pour résoudre des problèmes de probabilité.
3. Le cadre de dérivation des propositions logiques
Les diagrammes de Venn peuvent transformer des propositions logiques telles que « tous les A sont B » et « aucun A n'est C » en relations géométriques. Par exemple, dans le raisonnement syllogistique « tous les métaux sont conducteurs, le cuivre est un métal, donc le cuivre est un conducteur », en traçant un cercle de relation d'inclusion entre « métal » et « conducteur », la nécessité de la conclusion peut être rapidement vérifiée. Cette méthode de raisonnement graphique est également largement utilisée dans des domaines tels que l’algèbre booléenne et l’optimisation des requêtes de bases de données en informatique.
Statistiques sur la sélection des cours par les étudiants
Parmi 50 élèves d'une classe, 28 ont choisi le concours de mathématiques , 23 ont choisi le concours de chimie et 5 n'ont participé à aucun concours. Le modèle suivant peut être établi à travers le diagramme de Venn :
Statistiques de sélection des cours par les étudiants - Diagramme de Venn
Nombre total de participants = 50 - 5 = 45 ;
de Chimie et de Mathématiques = 28 + 23 = 51 ;
Nombre de participants dans les deux matières = 51 - 45 = 6.
Le diagramme de Venn final a montré : 22 personnes ont participé uniquement au concours de mathématiques , 17 personnes ont participé uniquement au concours et 6 personnes ont participé aux deux matières. Ce cas vérifie l'efficacité du diagramme de Venn dans la résolution du « problème de comptage de chevauchement ».
PPT/SmartArt : Convient pour dessiner rapidement des diagrammes de Venn de 2 à 3 ensembles de données. Vous pouvez générer des graphiques de base via « Insertion → SmartArt → Relation → Diagramme de Venn de base », qui prend en charge le réglage des couleurs et de la transparence.
Langage Origin/R : lorsque vous traitez plus de trois ensembles de données complexes, le plug-in Venn Diagram d'Origin ou le package ggVennDiagram du langage R peut générer des graphiques de haute précision.
Outil en ligne : ProcessOn, qui ne nécessite pas de remplissage de données et prend en charge le glissement direct de graphiques sur le canevas . Il convient aux utilisateurs sans connaissances en programmation.
Ensuite , en prenant ProcessOn comme exemple , nous allons présenter comment dessiner un diagramme de Venn :
Définir un ensemble : Accédez à la page du fichier ProcessOn, créez un nouvel organigramme et spécifiez l'ensemble à analyser (par exemple, sujet A, sujet B) ;
Dessinez des formes de base : cliquez sur « Plus de formes » à gauche, sélectionnez le diagramme de Venn, faites glisser deux cercles de la zone de forme vers le canevas et ajustez les positions afin qu'elles se chevauchent partiellement ;
Zone de marquage : remplissez les zones non superposées et les zones d'intersection avec des couleurs différentes et ajoutez des étiquettes de quantité d'éléments ;
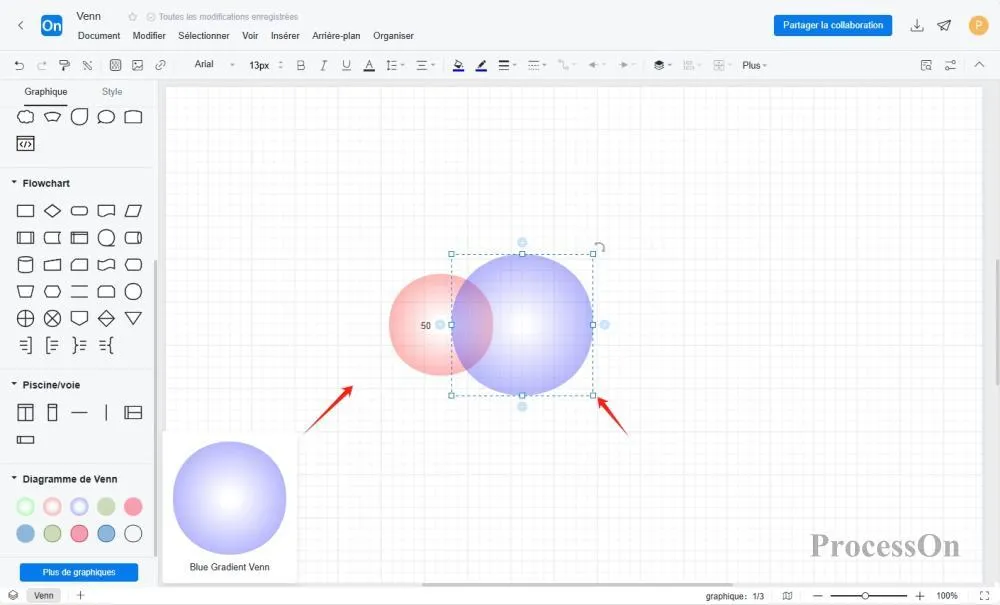
Optimiser l'affichage : ajuster la couleur, la transparence , etc. , et ajouter des descriptions textuelles telles que « uniquement A », « uniquement B », « A∩B », etc.
Télécharger ou partager : Après avoir dessiné le diagramme de Venn, vous pouvez cliquer sur le bouton de téléchargement dans le coin supérieur droit pour l'exporter vers des images, des PDF et d'autres formats, ou générer un lien en ligne à partager avec d'autres.
Bien que le diagramme de Venn ait l’avantage d’être intuitif, il convient également de noter ses limites :
Limitation du nombre d'ensembles : les diagrammes de Venn traditionnels peuvent afficher clairement jusqu'à 5 ensembles de données. Si le nombre dépasse ce chiffre, il est recommandé d’utiliser plutôt des diagrammes UpSet ;
Risque de distorsion de la surface : la surface du cercle peut ne pas être proportionnelle à la taille de l'ensemble, et le nombre spécifique d'éléments doit être marqué sur la figure ;
Non applicable aux données continues : pour les données continues telles que les séries chronologiques, les changements de température, etc., vous devez utiliser un graphique linéaire ou une carte thermique à la place.
Des opérations sur les ensembles en classe à l’analyse différentielle en génomique, le diagramme de Venn, avec son langage géométrique concis, transforme la logique mathématique abstraite en un modèle visuel perceptible. À mesure que la complexité des données augmente, l’application intégrée des diagrammes de Venn, des diagrammes UpSet, des diagrammes arborescents et d’autres outils conduit la visualisation mathématique à évoluer vers des dimensions supérieures. Pour les apprenants, maîtriser le dessin et l’application des diagrammes de Venn ne consiste pas seulement à maîtriser un outil, mais également à cultiver une pensée structurée et des capacités d’analyse interdisciplinaire.
Organigramme de carte mentale collaborative en ligne gratuit
