19 世紀、イギリスの数学者ジョン・ベンは、幾何学的図形を使用して集合の関係を表示するツール、ベン図を発明しました。重なり合う円を使って集合の交差、和集合、補集合を表すこの種のグラフは、数学の分野で基本的なツールとなっただけでなく、論理的推論、確率統計、データ分析においても強力な実用性を発揮しています。この記事では、定義、数学の応用シナリオ、典型的なケース、作成ツール、描画方法という 5 つの側面から、数学におけるベン図の核心価値を体系的に分析します。
ベン図は、重なり合う円形または楕円形の領域を通じて、複数のセット間の論理的な関係を視覚的に表現します。その中核となる要素は次のとおりです。
集合表現: 各円は独立した集合を表し、円内の領域は集合の要素です。
交差(∩):重なり合う領域は、2つ以上の集合の共通要素を表します。
和集合 (∪): すべての円で覆われた合計面積は、集合の和集合の結果を表します。
補集合: 円で覆われていない長方形のボックス (ドメイン) 内の領域は、どの集合にも属さない要素を表します。
例えば、集合A(数学が好きな生徒)と集合B(物理が好きな生徒)のベン図では、重なり合う部分は「数学と物理の両方が好きな生徒」、重なり合わない部分はそれぞれ「数学だけが好きな生徒」と「物理だけが好きな生徒」を表しています。
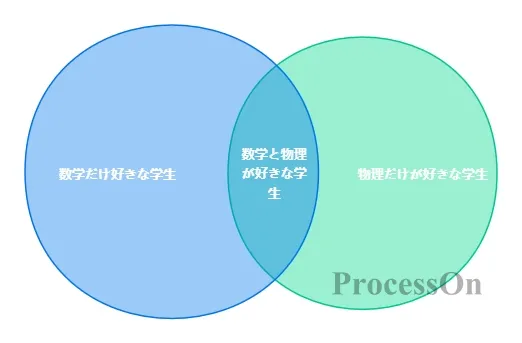
1. 直感的な集合演算
ベン図は抽象的な集合演算を視覚的な演算に変換します。たとえば、ド・モルガンの法則 ((A∪B)' = A'∩B') を証明する場合、2 つの集合の補集合と積集合をプロットすることによって等式を視覚的に検証できます。このグラフィカルな証明方法は、生徒が記号論理の認知的障壁を突破できるようにするために、初等数学教育で広く使用されています。
2. 確率問題のためのモデリングツール
確率論において、ベン図は独立した事象、相互に排他的な事象、条件付き確率の問題を解決するための強力なツールです。例えば、「サイコロを振って3より大きい偶数が出る」という確率を計算する場合、事象A(偶数:{2,4,6})と事象B(>3:{4,5,6})のベン図を描くことで、交差領域{4,6}の確率値を直接得ることができます。ケンブリッジ大学の研究によると、ベン図を使用した学生は確率の問題を解く効率が 40% 向上しました。
3. 論理命題の導出枠組み
ベン図は、「すべての A は B」や「どの A も C ではない」などの論理命題を幾何学的な関係に変換できます。例えば、「すべての金属は導体である、銅は金属である、したがって銅は導体である」という三段論法では、「金属」と「導体」の包含関係の円を描くことで、結論の必然性を素早く検証することができます。このグラフィカル推論法は、ブール代数やコンピュータサイエンスにおけるデータベースクエリ最適化などの分野でも広く使用されています。
学生のコース選択統計
クラスの生徒 50 人のうち、28 人が数学のコンテストを選択し、23 人が化学のコンテストを選択し、5 人はどのコンテストにも参加しませんでした。ベン図を通じて次のモデルを確立できます。
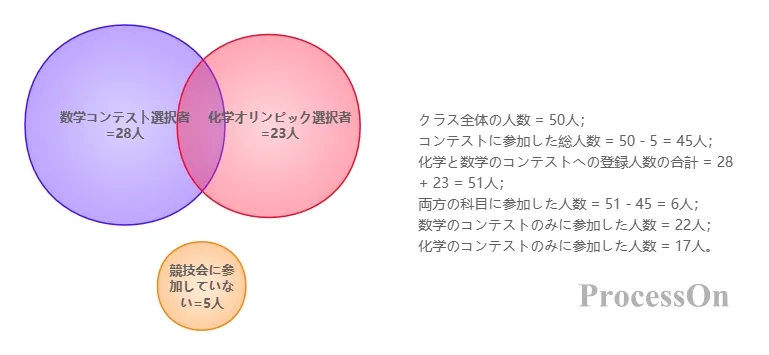
参加者総数 = 50 - 5 = 45;
化学と数学のコンテストの応募者数の合計 = 28 + 23 = 51;
両科目の参加者数 = 51 - 45 = 6。
最終的なベン図では、数学の競技のみに参加した人が 22 人、競技のみに参加した人が 17 人、両方の科目に参加した人が 6 人であることが示されました。この事例は、「重複カウント問題」を解決する際のベン図の有効性を検証します。
PPT/SmartArt: 2 ~ 3 セットのデータのベン図をすばやく描画するのに適しています。 「挿入 → SmartArt → リレーションシップ → 基本的なベン図」を通じて、色と透明度の調整をサポートする基本的なグラフィックを生成できます。
Origin/R 言語: 3 セット以上の複雑なデータを扱う場合、Origin のベン図プラグインまたは R 言語の ggVennDiagram パッケージを使用して高精度のグラフィックスを生成できます。
オンライン ツール: ProcessOn は、データの入力を必要とせず、グラフィックをキャンバスに直接ドラッグすることをサポートします。プログラミングの知識がないユーザーにも適しています。
次に、 ProcessOnを例に、ベン図の描き方を紹介します。
セットを定義する: ProcessOn ファイル ページに入り、新しいフロー チャートを作成し、分析するセット (件名 A、件名 B など) を指定します。
基本的な図形を描画する:左側の「その他の図形」をクリックし、ベン図を選択して、図形領域からキャンバスに2 つの円をドラッグし、部分的に重なるように位置を調整します。
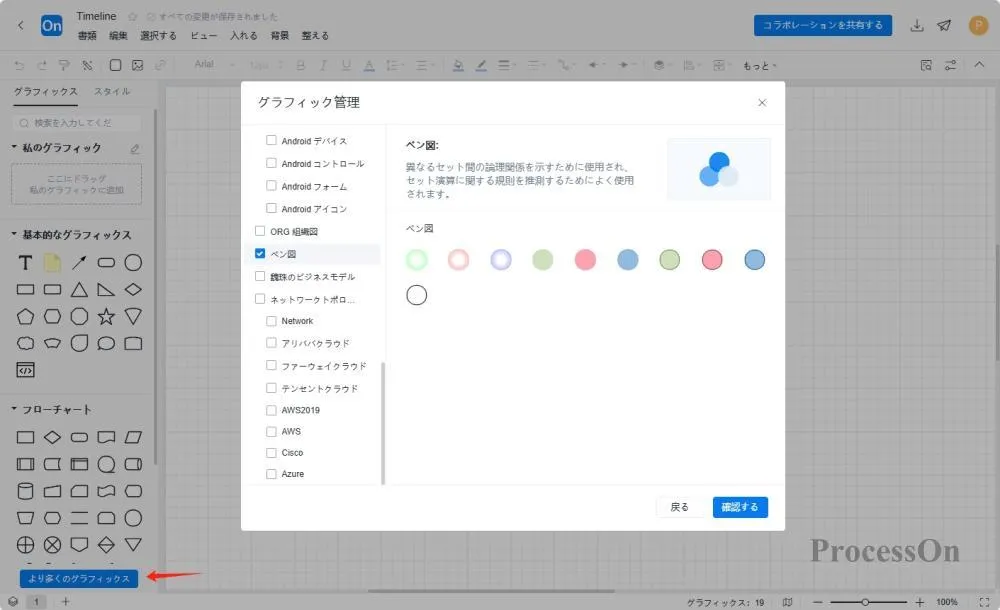
領域のマーキング: 重複しない領域と交差領域を異なる色で塗りつぶし、要素数量ラベルを追加します。
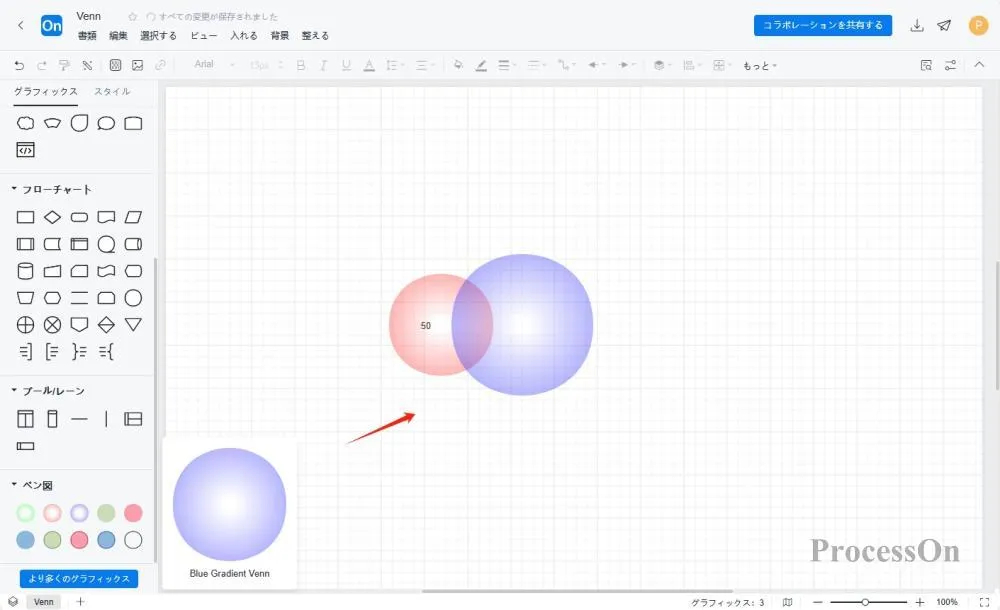
表示を最適化します。色、透明度などを調整し、「Aのみ」、「Bのみ」、「A∩B」などのテキスト説明を追加します。
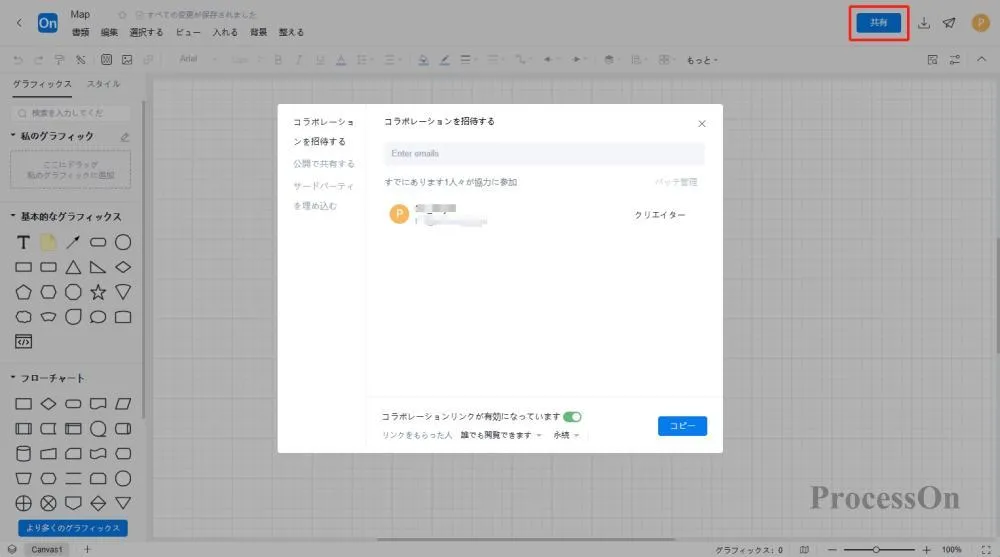
ダウンロードまたは共有: ベン図を描画した後、右上隅のダウンロード ボタンをクリックして、画像、PDF、またはその他の形式でエクスポートしたり、オンライン リンクを生成して他のユーザーと共有したりできます。
ベン図は直感的であるという利点がありますが、次のような限界もあることに注意する必要があります。
セット数の制限: 従来のベン図では、最大 5 セットのデータを明確に表示できます。数がこれを超える場合は、代わりに UpSet 図を使用することをお勧めします。
面積歪みのリスク:円の面積はセットのサイズに比例しない可能性があり、図には要素の特定の数をマークする必要があります。
連続データには適用されません: 時系列、温度変化などの連続データの場合は、代わりに折れ線グラフまたはヒート マップを使用する必要があります。
教室での集合演算からゲノミクスの差分分析まで、簡潔な幾何学的言語であるベン図は、抽象的な数学的論理を認識可能な視覚モデルに変換します。データの複雑さが増すにつれて、ベン図、UpSet 図、ツリー図などのツールを統合して適用することで、数学的視覚化はより高い次元へと進化しています。学習者にとって、ベン図の描き方と応用方法を習得することは、ツールを習得することだけでなく、構造化された思考と学際的な分析能力を養う重要な方法でもあります。