L型マトリックス：基本的な2次元表で、2つの要素の関係を示します。
T型マトリックス：L型マトリックスを3つの要素に拡張します（例：行、列、交差点の追加情報）。
X型マトリックス：4つの要素群の交差関係を分析します（例：品質、コスト、時間、リスクのバランス）。
Y型マトリックス：3つの要素間の双方向関係を示します（例：サプライヤー、製品、顧客のインタラクション）。

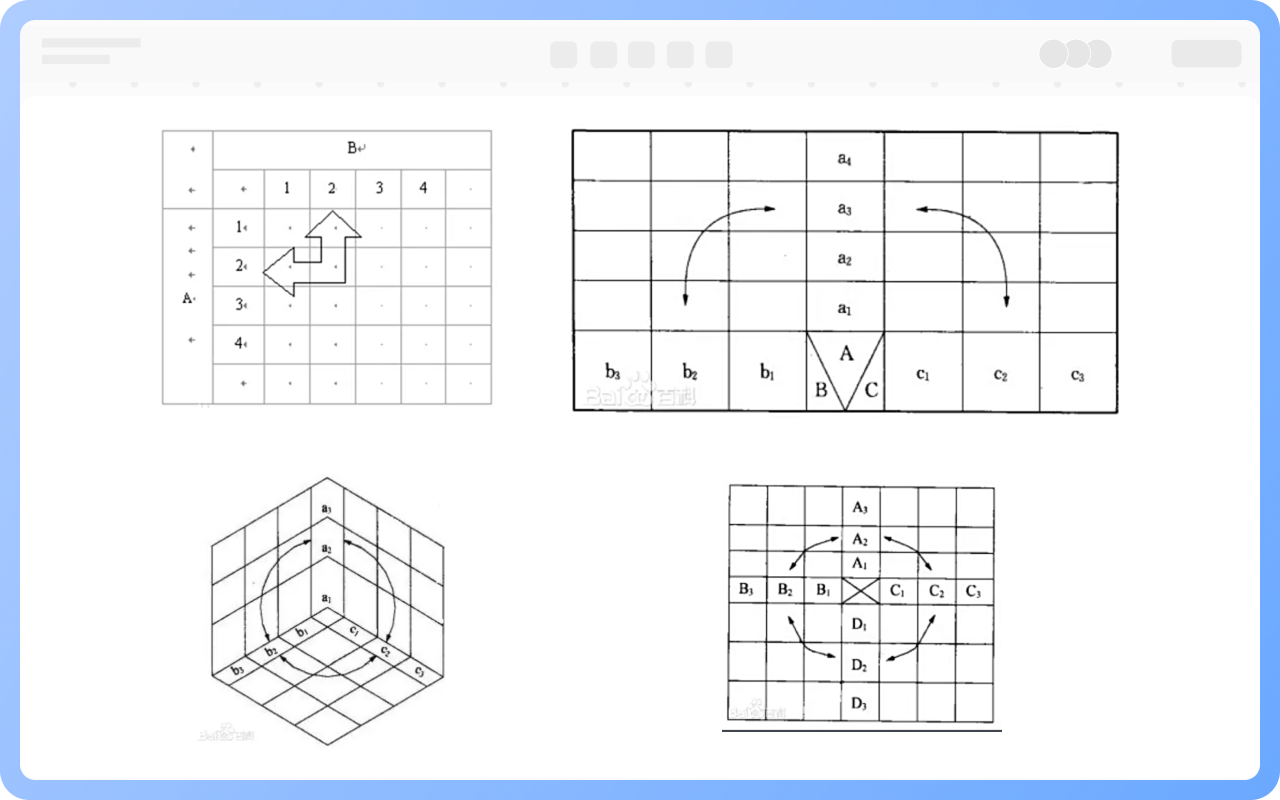
関係分析：要素間の関連性を明らかにします（例：タスクとリソースのマッチング、問題と原因の対応）。
比較表示：横または縦にデータの差異を比較します（例：地域別および製品別に分類された販売データの比較）。
優先順位の並べ替え：記号または数値で重要度をマークします（例：リスク評価マトリックスの高/中/低リスク）。
意思決定のサポート：多次元の意思決定を支援します（例：製品ポートフォリオの選択、投資プロジェクトの評価）。

多次元分析：2次元から4次元、さらには3次元の空間関係の分析をサポートし、さまざまな複雑度の問題シナリオに適応します。
関係の可視化：記号または数値で関係の強さを定量化し、重要な対応関係の見落としを避けます。
重点のフォーカス：交差点データに基づいて、優先的に制御すべき要素や問題点を迅速に特定し、問題解決の効率を向上させます。

1. ブレインストーミング、データ統計、または専門家の判断を通じて、問題に関連するすべての要素を網羅的に列挙します。
2. 要素群の数に応じて適切なマトリックスのタイプを選択します。たとえば、製品特性とテスト項目を分析する際にはL型マトリックスを使用します。
3. マトリックスの交点に記号（例：●、○、△）または数値（例：1-5点）を使用して要素間の関連度を示します。
4. 高い関連度の要素を統計し、優先的に制御すべき要素や問題点を特定します。
5. 重要な要素に対して具体的な制御計画や改善策を策定します。

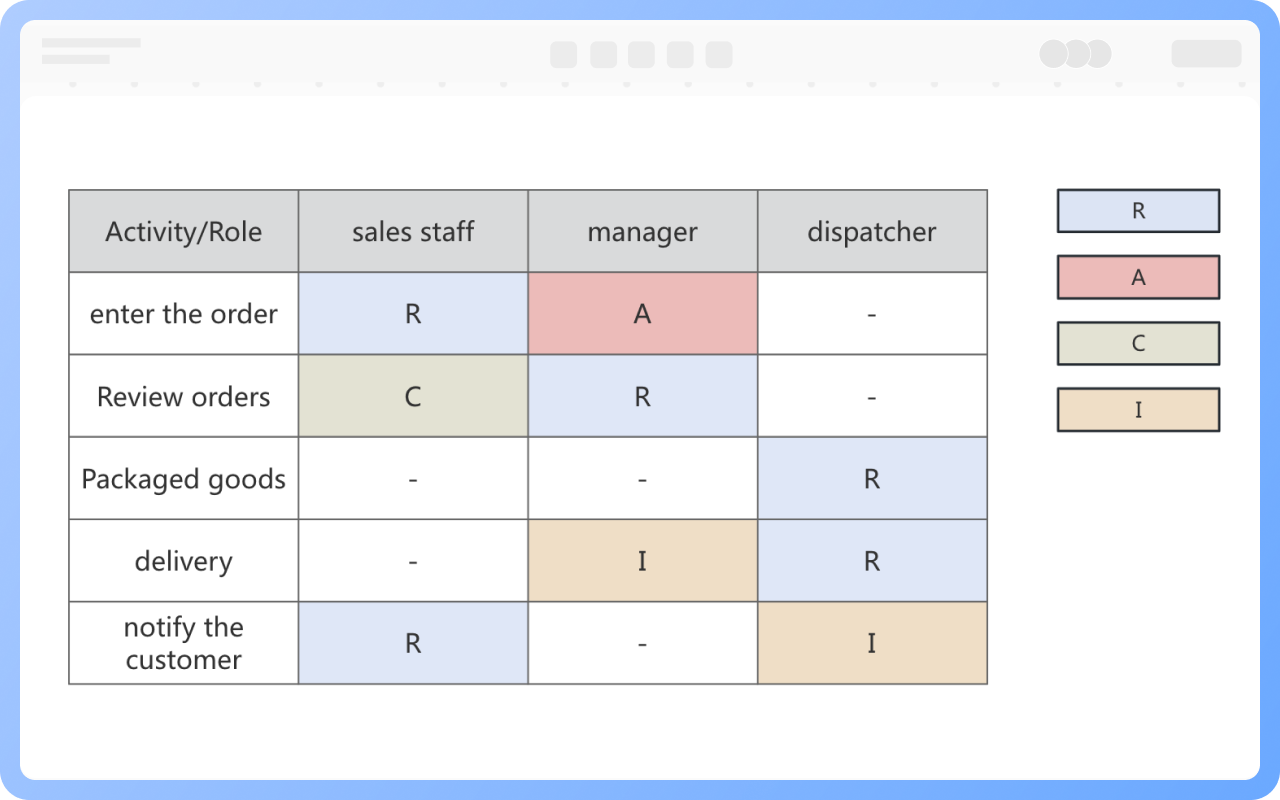
RACIマトリックスは責任分担マトリックスであり、プロジェクトやプロセスにおける各役割の責任と関与度を明確にするために使用されます。
RACIマトリックスの4つの文字は、それぞれ異なる役割の責任を表します：
R（Responsible）：タスクを実行する具体的な担当者で、具体的なアクション項目を完了する必要があります。1つのタスクには複数の実行者がいる場合があります。
A（Accountable）：タスクの結果に責任を持つ人で、通常は1人です。彼らは最終的な意思決定権とタスク完了の責任を持ち、彼/彼女の同意または署名があって初めてプロジェクトが進行できます。
C（Consulted）：タスクの実行過程で相談される必要がある人で、彼らの意見や提案はタスクの完了に重要な影響を与えます。これらの役割は通常、プロジェクトの完了に必要な情報や能力を持っています。
I（Informed）：タスクの進捗と結果を知らされる必要がある人で、通常はタスクの実行に直接関与しませんが、関連情報を理解してコミュニケーションの透明性を確保する必要があります。